Итерация свойственна человеку, а рекурсия — Богу.
Л. Питер Дойч
В программировании существуют приемы, которые кажутся простыми и стройными в теории, но на практике таят в себе большую опасность. Осознанность, полное понимание своих действий и их последствий — вот необходимое условие успеха при их использовании. Одним из таких приемов является рекурсия.
Рекурсивна любая сущность, если в ее определении присутствует ссылка на саму себя. В программировании чаще всего можно встретить рекурсию при определении функций. Рекурсивная функция — это функция, вызывающая саму себя. Определение функции (того, что она делает) не окончено, и эта неоконченная часть и служит вызовом определяемой функции.
Звучит не очень понятно, но на практике все довольно просто. Хрестоматийный пример использования рекурсии — вычисление факториала. Факториал целого числа представляет собой последовательное произведение этого числа и всех целых чисел, которые меньше его. Факториал нуля — единица. Факториал от N равен N, умноженному на факториал N - 1 или Fact(N) = N * Fact(N - 1). Это пример рекурсивного определения. Есть и более сложные примеры: алгоритм вычисления функции Аккермана, алгоритм Жордана—Гаусса для решения системы линейных уравнений, алгоритм поиска наибольшего общего делителя.
Следующий листинг на языке программирования Си демонстрирует простую реализацию алгоритма вычисления факториала:

Если функция вызывается с параметром, меньшим или равным нулю, то возвращается единица. Это — нерекурсивная часть функции. В любом другом случае будет вызвана эта же функция с параметром на единицу меньше первоначального, а результат ее выполнения будет умножен на первоначальный параметр.
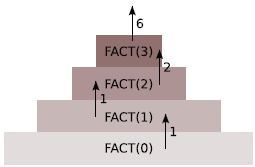
Использование рекурсии дает быстрый и наглядный результат. У рекурсии, однако, есть и «темная сторона».
Один из главных минусов заключается в том, что рекурсивный алгоритм очень часто не гарантирует конечной глубины рекурсии. В случае факториала заметно, что рекурсия конечна. Но при реализации более сложных алгоритмов возможны проблемы «зацикливания» рекурсивных вызовов, и программист должен убедиться, что этого не случится. Существует опасность, что функция так и не вернет управление, а будет бесконечно вызывать саму себя. Однако в большинстве языков программирования вечного цикла таким образом не получится. Раньше случится переполнение стека. Дело в том, что при вызове любой функции все переменные в текущей области видимости (читай — определенные в текущей функции) скрываются локальными переменными вызванной функции, но никуда не удаляются. Кроме того, стек расходуется на то, чтобы передать параметры вызываемой функции и вернуть возвращаемое значение.
К счастью, в практике программирования очень мало задач, которые можно решить только рекурсией. Итеративный подход хоть и лишен божественности, согласно эпиграфу, но более универсален и практичен с точки зрения компьютерной науки.
Ниже приведен пример итеративной реализации алгоритма вычисления факториала:

Текст функции стал немного длиннее, и пропала наглядность, но теперь единственный возможный вид переполнения — это арифметическое переполнение, так как факториал от 13 уже не умещается в самое большое встроенное целое на 32-битном компьютере. Придется либо использовать типы, аналогичные int64, либо обращаться к математическим библиотекам повышенной точности, позволяющим оперировать действительно огромными числами. При итеративном подходе переполнение стека нам не угрожает: рекурсивный вызов заменяется циклом и не нужно «откладывать» текущую копию локальных переменных в стек.
Но не спешите списывать со счетов рекурсивную реализацию алгоритмов. Она пригодится в таких областях, как искусственный интеллект. Без рекурсии не обойтись при реализации генетических и метагенетических алгоритмов, используемых при построении систем, способных к обучению.
Функциональные языки программирования, а точнее, их интерпретаторы и компиляторы способны даже оптимизировать хвостовую рекурсию и преобразовывать ее в итерации.
Кроме программирования рекурсия существует в математике, физике и даже лингвистике. Все геометрические фракталы задаются с помощью бесконечной рекурсии, а алгоритм решения задачи о Ханойских башнях на самом деле рекурсивный. Существуют даже рекурсивные аббревиатуры, например GNU: «GNU’s not Unix». Но это уже совершенно другая история.