«Компьютер никогда не ошибается!» — скажет кто-то и будет в какой-то мере прав. Но каждый настоящий «компьютерщик», конечно, знает, что программы пишут люди, а уж они-то ошибаются! Да и как человек может создать программу, которая будет играть лучше своего создателя? Вопросик…
Попробуем разобраться на примере некоторых общеизвестных игр. Но учтите, что все сказанное будет верно лишь для логических игр с полной информацией, т. е. таких, в которых ничего не отдается на волю случая (предвижу огорчение любителей эротического покера), а результат зависит от мыслительных способностей соперников.
Секрет победы
Каждая компьютерная программа создавалась прежде всего как модель нашего с вами поведения. Что занимает человека более всего во время игры? Какие мысли и действия приведут его к победе? О чем думает победитель? Эти вопросы волновали разработчиков игровых программ во время их работы над своими творениями.
Насколько велик набор средств, приносящих победу?
Можно втихаря пнуть под столом противника по коленке. Тогда он, безусловно, расстроится и совершит какую-нибудь ужасную ошибку, которая позволит нам выиграть. Можно иными способами воздействовать на психику оппонента, выводя его из себя и заставляя ошибаться. Есть вариант со снотворным в лимонаде соперника…
А если играть честно? Тогда ничего другого нам не остается…
Иерархический перебор лежит в основе любого человеческого способа выбора хода в позициях игры: «Если я пойду так, то возникнет позиция, где у меня будут вот такие возможности, но противник может ответить так-то и так-то, а я ему на это…» — типичное обоснование выбора хода (с некоторыми вариациями) даже для очень хорошего шахматного гроссмейстера. Ясно, что такое обоснование подразумевает всего-навсего перебор вариантов.
В зависимости от своих способностей и опыта человек оценивает позицию, определяет наиболее перспективные ходы, просматривает предполагаемые ответы соперника, выбирает новые хорошие ходы, ищет лучшие ответы соперника… Этот процесс останавливается лишь тогда, когда игрок получает ясную для него позицию (например, съел последнюю шашку соперника или просто получил заведомо выигрышную позицию с лишним ферзем) или… тогда, когда запутался во множестве вариантов, не смог больше держать в памяти огромное количество ходов и получающихся из них позиций, а перед глазами бешено проносятся слоны, крутятся дамки, ковыляют короли, скачут кони и шашки бросаются поедать друг друга… В общем, человек устал.
Ага! Вот оно! Теперь мы знаем, как побеждают в логических играх: перебирая варианты ходов и оценивая получаемые позиции, а также знаем, почему проигрывают: человек устает, пропускает хорошие варианты и теряет способность правильно оценивать положение на доске. Однако перебор вариантов — это то, что лучше всего получается у компьютеров, а усталость им просто неведома! Вот мы и нашли рецепт непобедимой компьютерной программы.
Таким образом, если мы сможем запрограммировать полный перебор всех вариантов (от начальной позиции до победной), то мы создадим совершенную программу, которую никто не сможет обыграть!
Так не будем терять времени и приступим к этому прямо сейчас.
Победоносный перебор
Чтобы детально во всем разобраться, возьмем какую-нибудь интеллектуальную игру попроще и рассмотрим, как нужно организовать перебор вариантов, чтобы побеждать (или хотя бы не проигрывать) всегда и всех.
Что у нас есть из самого простого? Вот! Крестики-нолики на поле 3×3.
Чтобы описать процесс перебора вариантов ходов в игре, мы будем создавать дерево игры, в котором вершины будут представлять собой возникающие в игре позиции, а дуги — определять ходы каждого из соперников.
Исходную позицию в игре все знают (рис. 1).

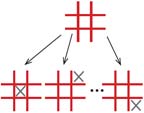
Первым ходит игрок, который ставит крестики, ему доступна любая клетка поля (рис. 2).
Ответ соперника приходится на любое из оставшихся полей (рис. 3).
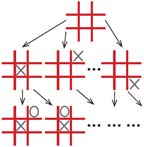
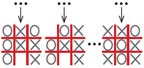
 И заканчивается игра тогда, когда один из игроков побеждает, создав ряд по диагонали, горизонтали или вертикали, заполненный его значками, либо когда победителя нет — ничья (рис. 4).
И заканчивается игра тогда, когда один из игроков побеждает, создав ряд по диагонали, горизонтали или вертикали, заполненный его значками, либо когда победителя нет — ничья (рис. 4).
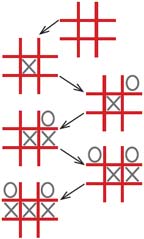
Таким образом, переходя по стрелкам от вершины до самых последних позиций, мы получим одну из возможных партий в крестики-нолики (рис. 5).
Конечно, количество вариантов развития игры слишком велико, чтобы можно было перечислить и записать их все вручную. Человек провел бы не одни сутки, непрерывно составляя полное дерево игры! Но ведь для современных компьютеров эта задача не будет слишком сложна?
Точно так же можно составить дерево игры для шашек и шахмат.
При анализе позиции компьютерная программа должна по порядку перебрать все доступные шашки или фигуры соответствующего цвета и совершить ими все возможные в их положении ходы из данной позиции. Естественно, что в каждой из исходных позиций имеется конечное (и сравнительно небольшое) количество допустимых ходов (в шашках обычно пять — семь, но, скажем, в эндшпиле при наличии дамок количество вариантов существенно вырастет; в шахматах на каждую позицию приходится по 20—30 ходов).
Любое перемещение шашки или фигуры будет приводить к новой позиции, в которой право хода принадлежит противоположной стороне. Таким образом, имея некоторую начальную позицию, программа способна воспроизвести на ее основе множество других возможных позиций, которые могут возникнуть через один полуход (ход одного из соперников).
Отсекая варианты своих ходов, приводящие к проигрышу, мы получим позиции и соответствующие им ходы, следуя которым никогда не проиграем (безусловно если только это возможно).
Все хорошее когда-нибудь заканчивается…
Понятно, что перебрать все позиции игры в крестики-нолики на поле 3×3 можно: изначально доступны всего девять полей, с каждым ходом одного из противников доступных полей становится меньше до тех пор, пока кто-нибудь не выиграет или не будут заполнены все поля.
Однако в других играх однажды возникшая позиция может повториться, кроме того, в шахматах, например, фигуры практически не ограничены в своих перемещениях по игровому полю. Так можно ли применить метод перебора к другим играм, таким как шашки или шахматы? Можно. И шашки и шахматы содержат правила, гарантирующие, что игра когда-нибудь закончится. В шашках ничья присуждается, если соотношение сил на доске не изменилось в течение 60 ходов (а то и меньше, в зависимости от количества шашек на доске), а в шахматах — если за 50 ходов не было сделано ни одного взятия фигуры или хода пешкой. Поэтому даже самая длинная партия (шахматная партия, например, может состоять максимум из 6350 ходов! Но столько до сих пор еще никто не играл) когда-нибудь закончится, а это значит, что наш перебор завершится и мы сможем узнать результат игры с идеальным партнером (который никогда не ошибается) еще до самого первого хода.
Тень сомнения
«Неужели все так просто?» — воскликнет недоверчивый читатель. А кто-то вспомнит, что «непобедимая» шашечная программа появилась совсем недавно, а про шахматный идеал вообще пока даже речи не идет…
Вы правы! Специалисты, занимающиеся созданием компьютерных программ, способных побеждать лучших из играющих людей, давно знают, что самая простая и самая грубая попытка перебора всех возможных вариантов ходов не приведет их к успеху… Почему? Вот об этом мы подробнее поговорим в следующей части нашего рассказа.
С автором можно связаться по адресу: wit9@yandex.ru.
Немного истории
В 1770 г. Вольфганг (Фаркаш) фон Кемпелен создал при дворе австрийской императрицы Марии-Терезии шахматный «автомат», который затем в течение 70 лет будоражил умы шахматистов сначала Европы, а затем и Америки, побеждая многих из сильнейших игроков того времени. Лишь в 1836 г. стало общеизвестно, что внутри «автомата» всегда прятался человек.
В 1967 г. состоялся первый матч шахматных программ (теперь уже действительно программ). С этого момента в шахматной компьютерной гонке приняло участие множество самых одаренных людей. Компьютерные шахматы стали практически синонимом «искусственного интеллекта», а в 1997 г. компьютерная программа выиграла (хотя и спорно) матч у Гарри Каспарова — чемпиона мира по шахматам.
В 2007 г. журнал Science сообщил о том, что группой исследователей из университета провинции Альберта (Канада) создана программа Chinook, которую невозможно обыграть в шашки.
Анекдот
1977 г., чемпионат среди компьютеров по игре в шахматы.
Вечером после очередного тура представитель советской команды прокрадывается в компьютерный зал, засовывает в дисковод самого большого советского компьютера тарелку супа и шепчет: «Гарри1, ты как?»
1Гарри Каспаров — с 1985 по 1993 г. (по версии Профессиональной шахматной ассоциации — по 2000 г.) чемпион мира по шахматам среди людей.