В предыдущей статье, посвященной клеточным автоматам (см. «Мир ПК», № 8/03), речь шла о «черно-белых» автоматах. На этот раз мы рассмотрим свойства клеточных автоматов с б?ольшим числом состояний, каждому из которых может быть поставлен в соответствие определенный цвет спектра.
— Белый — это цвет?
— Да.
— Черный — это цвет?
— Да.
— Почему ты тогда говоришь,
что это не цветной телевизор?
Из фольклора
Что понимается под «цветными» клеточными автоматами
Наряду с «черно-белыми» клеточными автоматами, рассмотренными в статье [1], существуют «цветные» автоматы [2], клетки которых могут находиться более чем в двух состояниях. При этом каждой клетке соответствует целочисленная переменная, кодирующая ее состояние в данный момент времени. В компьютерных системах цвет обычно представляется целым числом. Поэтому каждому состоянию клетки автомата может быть поставлен в соответствие конкретный цвет спектра.
Связь между цветами и целыми числами обеспечивается разными способами, например RGB-кодированием [3], при котором соответствующее цвету число составляется из трех последовательных байтов (дескриптор цвета), показывающих насыщенность красного (Red), зеленого (Grеen) и синего (Blue) цветов.
Несмотря на то что хранение такого дескриптора требует 24 битов (три байта), представляющий его тип данных занимает 32 бита (четыре байта). Это отчасти связано с необходимостью выравнивания адресов по степеням двойки [4]. Например, в Visual C++ тип данных для цветового дескриптора имеет имя COLORREF [5]. «Лишний» байт обычно называют байтом прозрачности и не учитывают.
В результате изображение, в котором цвет каждого пиксела описывается 24 битами, можно рассматривать как 24-битовые плоскости. Каждая из этих плоскостей является решеткой двумерного битового клеточного автомата. Такие автоматы описаны в статье [1].
При визуализации будем изображать единую «цветную» решетку. Цвет каждой ее клетки последовательно «собирается» из битов состояний клеток 24 битовых решеток, имеющих одно и то же положение с соответствующей цветной клеткой. Таким образом, 24-битовый цветовой дескриптор формируется из 24 последовательных битов.
Отсюда следует, что в любом случае совокупность 24 битовых клеточных автоматов может быть заменена одним автоматом, множество состояний каждой клетки которого совпадает с множеством значений цветового дескриптора. Это означает, что каждая клетка может быть в одном из 224 состояний, закодированных числами от 0 до 224 - 1.
Далее мы рассмотрим клеточные автоматы с принципиально различными функциями переходов [1, 3]. В трех первых примерах множество состояний каждой клетки заметно меньше множества значений цветового дескриптора, поэтому ее функция переходов может быть задана с помощью набора из нескольких условий. Четвертый и пятый примеры характеризуются тем, что каждый из 24-битовых автоматов, составляющих «цветной» клеточный автомат, должен быть рассмотрен отдельно. Поэтому в функции переходов производится разбиение значения цветового дескриптора на биты. В шестом примере отдельно рассматриваются только первый и второй биты цветового дескриптора.
Иногда удается записать функцию переходов клетки с помощью арифметических, логических или поразрядных операций над 24-битовыми целыми числами, не прибегая к разбиению и анализу отдельных битов. В седьмом примере показано, что с помощью поразрядной операции «сумма по модулю 2» над значениями определенных переменных можно реализовать клонирование данных из некоторой области решетки («генерировать копии самих себя» [6]). Эти переменные кодируют состояния самой клетки и четырех ее соседей, имеющих с ней общие стороны (так называемых «главных» соседей). Для наглядности в качестве начальных условий авторами выбрано изображение Моны Лизы.
Реализация «цветных» клеточных автоматов
Программа, визуализирующая работу «цветного» клеточного автомата, имеет следующую структуру.
- Вводится два массива дескрипторов цвета для хранения состояний клеток. Первый из них содержит текущее состояние каждой клетки автомата, а второй предназначен для хранения нового ее состояния.
- Определяется функция переходов клетки решетки. В качестве параметров в функцию переходов передаются текущие значения состояний клеток окрестности, возможно, включая ее саму. Эта функция может быть задана в виде выражения над дескрипторами цвета как целыми числами. При вычислении этой функции может возникнуть необходимость рассматривать каждую составляющую плоскость битов отдельно.
- На нулевом шаге производится заполнение решетки (первого массива) начальными данными.
- вычисления новых состояний вводится цикл. На каждой итерации для каждой клетки, используя в качестве аргументов функции переходов элементы первого массива, вычисляют ее новое состояние, которое помещают во второй массив.
- После завершения итерации значения из всех элементов второго массива переносят в первый. Этим обеспечивается псевдопараллельное изменение значений состояний всех клеток решетки.
- Осуществляется визуализация содержимого первого массива.
- Пользователь с помощью соответствующих элементов управления либо обеспечивает переход к следующему шагу (пункту 4), либо прекращает работу программы.
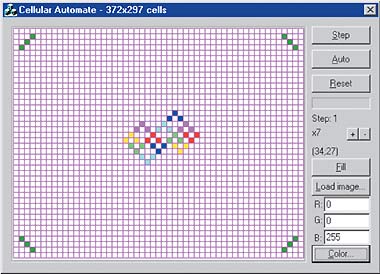
На рис. 1 показан пользовательский интерфейс разработанной программы.
|
| Рис. 1. Пользовательский интерфейс программы |
Приведем назначение элементов управления:
- кнопка "Step" обеспечивает выполнение одного шага клеточного автомата;
- кнопка "Auto" переводит программу в режим автоматического выполнения шагов и выводит из него при повторном нажатии;
- кнопка "Reset" обеспечивает восстановление начального состояния программы и моделируемого клеточного автомата (инициализация);
- индикатор выполнения процесса показывает ход выполнения текущей задачи (шага, инициализации и т. п.);
- поле "Step" отображает номер текущего шага клеточного автомата;
- поле для отображения текущей степени увеличения (размера представления клеток решетки);
- кнопки "+" и "-" увеличивают и уменьшают размер представления клеток решетки; при увеличении более чем в 5 раз отображается вспомогательная сетка;
- поле для отображения координат клетки решетки, над которой в данный момент находится указатель мыши;
- кнопка "Fill" обеспечивает заполнение всех клеток решетки текущим цветом;
- кнопка "Load image..." обеспечивает загрузку из файла и заполнение клеток решетки битовым представлением обрабатываемого графического изображения; маленькое изображение на решетке будет размещено по центру;
- поля ввода "R", "G" и "B" позволяют задавать текущий цвет покомпонентно;
- кнопка "Color" позволяет выбрать текущий цвет с помощью диалога.
На основе изложенного авторами разработаны программы на языке Cи++, иллюстрирующие каждый из приводимых ниже примеров. Эти программы можно загрузить с сайта http://is.ifmo.ru (раздел «Статьи»). Все программы однотипны и отличаются только (кроме примера 6) двумя функциями, специфичными для каждого конкретного автомата. Ими являются функция init(), задающая начальные условия, и функция переходов f(y, yU, yUR, yR, yDR, yD, yDL, yL, yUL). Обе они принадлежат классу CCADlg. При этом ниже для каждого примера будут приведены только эти две функции.
Примеры автоматов с функцией переходов, заданной в виде набора условий
Пример 1. В работе [7] для иллюстрации понятия «клеточный автомат» приведен пример «цветного» клеточного автомата, каждая клетка которого может быть в одном из четырех состояний, закодированных числами (цветами): 0 (белый), 1 (красный), 2 (зеленый) и 3 (синий). Окрестность каждой клетки составляют четыре ее главных соседа. Функция переходов в этом случае задается следующими правилами:
- если клетка находится в состоянии 0 и лишь одна из окрестных клеток находится в состоянии 1, то она переходит в состояние 2;
- если клетка находится в состоянии 0 и лишь одна из окрестных клеток находится в состоянии 2, то она переходит в состояние 3;
- если клетка находится в состоянии 0 и все четыре окрестные клетки находятся в состоянии 3, то она переходит в состояние 3;
- если клетка находится в состоянии 1 и хотя бы одна из окрестных клеток находится в состоянии 3, то она переходит в состояние 3;
- если клетка находится в состоянии 2 и хотя бы одна из окрестных клеток находится в состоянии 3, то она переходит в состояние 3.
Введем массив s[4], который задает соответствие между номерами состояний и цветовыми дескрипторами, определяющими белый, красный, зеленый и синий цвета:
COLORREF s[4]={RGB(255,255,255),RGB(255,0,0),
RGB(0,255,0),RGB(0,0,255)};В качестве начальных условий выбран красный крест из пяти клеток на белом поле:
void CCADlg::init()
{
for (WORD ww=0; wwДля вычисления функции переходов введем вспомогательную функцию count(y1,y2,y3,y4,s), позволяющую определить, сколько клеток из y1, y2, y3 и y4 находится в состоянии s:
inline BYTE count(COLORREF y1,COLORREF y2,
COLORREF y3,COLORREF y4,COLORREF s)
{
BYTE b=0;
if (y1==s) b++;
if (y2==s) b++;
if (y3==s) b++;
if (y4==s) b++;
return b;
}
При этом функция переходов может быть записана следующим образом:
COLORREF CCADlg::f(COLORREF y, COLORREF yU,
COLORREF yUR, COLORREF yR, COLORREF yDR,
COLORREF yD, COLORREF yDL, COLORREF yL,
COLORREF yUL)
{
if (y==s[0]) {
if (count(yU,yR,yD,yL,s[1])==1) return s[2];
if (count(yU,yR,yD,yL,s[2])==1 ||
count(yU,yR,yD,yL,s[3])==4) return s[3];
}
if (y==s[1]) {
if (count(yU,yR,yD,yL,s[3])>=1) return s[3];
}
if (y==s[2]) {
if (count(yU,yR,yD,yL,s[3])>=1) return s[3];
}
return y;
}
При использовании приведенных выше функций автомат отличается весьма «скучным» поведением. После пятого шага состояние решетки не изменяется — автомат переходит в статическое состояние. Состояния решетки этого автомата изображены на рис. 2.

|
| Рис. 2. Поведение автомата (пример 1 — простой крест) |
Пример 2. Отметим, что добавление к правилам лишь одного условия позволяет сделать поведение автомата более интересным — периодическим:
- если клетка находится в состоянии 3 и все четыре окрестных клетки находятся в состоянии 3, то она переходит в состояние 1.
Состояния решетки, получающиеся в этом случае при тех же начальных условиях, что и в примере 1, приведены на рис. 3. Конфигурации, приведенные для шестого и седьмого шагов, повторяются и далее, сменяя друг друга. Таким образом, начиная с шестого шага имеет место периодическое поведение с периодом 2.

|
| Рис. 3. Периодическое поведение автомата (пример 2 — периодический крест) |
Пример 3. Если к правилам автомата из примера 1 добавить другое условие (относительно примера 2), то автомат демонстрирует самовоспроизведение:
- если клетка находится в состоянии 3 и хотя бы одна из окрестных клеток находится в состоянии 1, то она переходит в состояние 1.
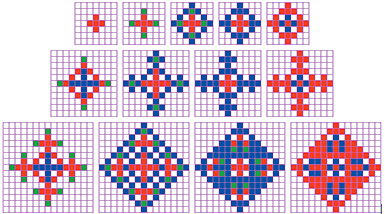
Состояния решетки, получающиеся в этом случае при тех же начальных условиях, что и в примере 1, приведены на рис. 4.
|
| Рис. 4. Самовоспроизведение (пример 3 — самовоспроизводящийся крест) |
Самовоспроизведение в рассматриваемом примере состоит в следующем: на красных окончаниях появляются зеленые «хвостики», которые превращаются в синие «цветы». «Созревая», они становятся красными и образуют новые окончания.
Цветная «Жизнь»
Рассмотрим двумерную решетку, каждая клетка которой может содержать 24-битовое число в виде 24 отдельных битовых плоскостей. На каждой из них реализуем игру «Жизнь» [1, 8]. При этом функция переходов должна быть написана так, чтобы каждая плоскость рассматривалась независимо от других (см. листинг 1).
Работу цветной игры «Жизнь» проиллюстрируем двумя примерами полетов планеров [8].
Пример 4. Пусть на решетке размещены три планера, ориентированные на столкновение. Они не должны иметь общих единичных битов в числовых представлениях цвета. Поэтому выберем следующие цвета (в RGB-представлении): красный (255, 0, 0), зеленый (0, 255, 0) и синий (0, 0, 255).
Цветной планер представляет собой «эскадрилью» из восьми «классических» планеров [8], каждый из которых летит в своей плоскости.
С учетом указанного выбора цветов это позволяет добиться того, что никакие два из 24 планеров не будут «лететь» в одной плоскости. В результате при столкновении цветные планеры пролетят один сквозь другой.
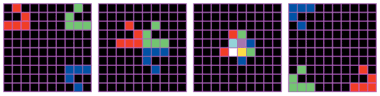
Полет цветных планеров изображен на рис. 5. На этом рисунке приведены кадры, соответствующие начальному, 8-му, 12-му и 28-му шагам автомата.
|
| Рис. 5. Полет цветных планеров (пример 4) |
Пример 5. Рассмотрим столкновение двух цветных планеров, в результате которого «выживает» лишь один из них, изменив при этом цвет.
Разместим на плоскости желтый (255, 255, 0) и красный (255, 0, 0) планеры, ориентированные на столкновение. Желтый планер представляет собой эскадрилью из 16 планеров, верхние восемь из которых сталкиваются с эскадрильей красного планера.
В результате из желтого планера получим зеленый (0, 255, 0), а также «обломки» красного цвета.
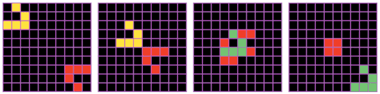
Полет цветных планеров, рассматриваемых в настоящем примере, изображен на рис. 6. На этом рисунке приведены кадры, соответствующие начальному, 8-му, 12-му и 28-му шагам автомата.
|
| Рис. 6. Полет цветных планеров (пример 5) |
Игра «Жизнь с историей»
Как отмечалось выше, в «цветных» клеточных автоматах рассматриваемого типа используются 24 битовые плоскости. Реализуем в первой из них классическую игру «Жизнь». При этом результат каждой предыдущей итерации будем переносить на следующую по порядку битовую плоскость. Таким образом, автомат будет «помнить» историю последних 32 итераций, а отображать историю последних 24 итераций.
Поскольку цветовой дескриптор хранит информацию в порядке «синий, зеленый, красный», «взведенному» биту на первой плоскости соответствует темно-синий цвет (0, 0, 128 в RGB-представлении).
Пример 6. Для того чтобы реализовать игру «Жизнь с историей», в визуализирующей программе произведено существенное изменение: перед каждой следующей итерацией осуществляется сдвиг всех значений состояний, полученных на предыдущей итерации, на один бит вправо. Эту операцию невозможно выполнить в функции переходов, поэтому она выполняется отдельно.
Функция переходов разместит информацию о текущей итерации на первой плоскости. При этом информацию о предыдущей итерации она получит со второй плоскости. Функция может быть реализована следующим образом (см. листинг 2).
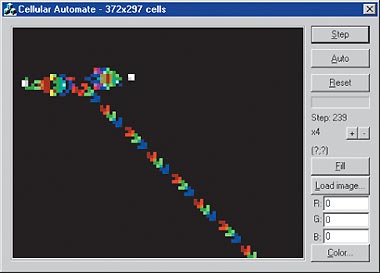
В качестве начальных условий выберем планерное ружье [8] белого цвета (255, 255, 255). Результат его эволюции после 239 итераций приведен на рис. 7.
|
| Рис. 7. «Жизнь с историей» на примере эволюции планерного ружья (пример 6) |
Клетки, имеющие красные составляющие, были живы от 17 до 24 итераций назад, клетки с зелеными составляющими — от 8 до 16, а с синими — от настоящего момента до 7 итераций назад.
Отметим, что «Жизнь с историей» дает возможность исследования поведения популяций в классической игре «Жизнь» [1, 8]. Она позволяет наглядно выявлять некоторые статические, периодические и вымирающие участки популяций. Так, в обычной игре «Жизнь» в текущий момент времени можно было бы наблюдать лишь то, что происходит в цветной игре на первой битовой плоскости.
Клонирование Моны Лизы
Разработанная визуализирующая программа позволяет воспроизводить (но не подделывать!) и произведения искусства. На примере картины Леонардо да Винчи «Мона Лиза» покажем, как клонируются мировые шедевры.
Пример 7. Выберем в качестве функции переходов операцию «сумма по модулю 2» для тех значений переменных, которые кодируют состояния самой клетки и четырех ее главных соседей.
Функция имеет вид:
COLORREF CCADlg::f(COLORREF y, COLORREF yU,
COLORREF yUR, COLORREF yR, COLORREF yDR,
COLORREF yD, COLORREF yDL, COLORREF yL,
COLORREF yUL)
{
return y^yU^yR^yD^yL;
}
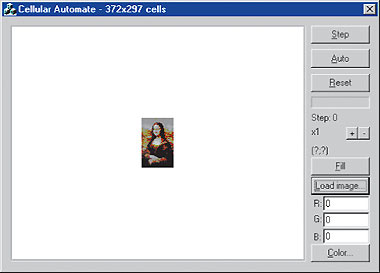
С помощью кнопки «Load Image...» загрузим BMP-файл, хранящий картину размером 41 х 64 пиксела (рис. 8).
|
| Рис. 8. Мона Лиза. Шаг 0 |
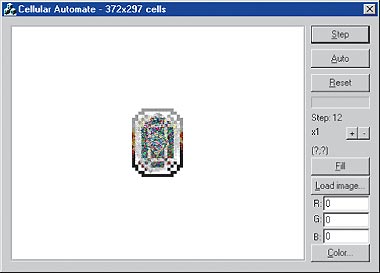
На 12-м шаге (рис. 9) Мону Лизу уже не узнать.
|
| Рис. 9. Мона Лиза. Шаг 12 |
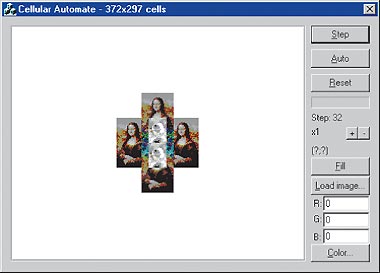
На 32-м шаге (рис. 10) становятся очевидными очертания пяти Мон Лиз.
|
| Рис. 10. Мона Лиза. Шаг 32 |
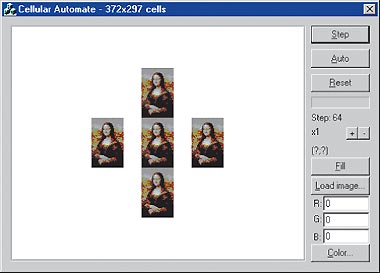
На 64-м шаге (рис. 11) клонирование завершено — получено пять Мон Лиз. В работе [1] приведено соотношение, показывающее, что клонирование должно завершиться именно на этом шаге.
|
| Рис. 11. Мона Лиза. Шаг 64 |
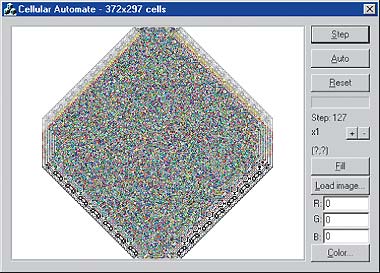
На 127-м шаге имеет место состояние решетки, которое можно принять за хаотическое (рис. 12).
|
| Рис. 12. Мона Лиза. Шаг 127 |
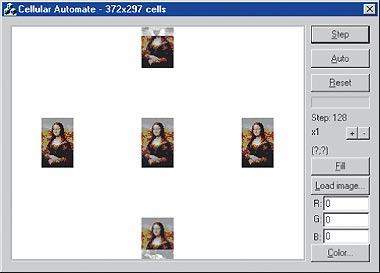
На следующем шаге появляется очередной результат клонирования — снова пять Мон Лиз (рис.13).
|
| Рис. 13. Мона Лиза. Шаг 128 |
На этом рисунке верхняя и нижняя Моны Лизы помешали друг другу полноценно развиться за счет малой размерности решетки и «заворачивания» ее в тор.
Обоснование клонирования для случая битового автомата приведено в работе [1]. В «цветном» случае тот же эффект имеет место на каждой из 24 битовых плоскостей, что при визуализации дает цветное изображение.
Вместо заключения
Настоящая работа является едва ли не единственной научно-популярной статьей, посвященной автоматам, клетки которых могут быть в большом числе состояний. Благодаря книге М. Гарднера [8] даже школьники знают о черно-белой игре «Жизнь», но в настоящей работе эта игра расцвечена новыми красками.
Множество задач, которые можно решать с помощью «цветных» клеточных автоматов, необозримо. Например, обработка изображений, моделирование физических процессов, распознавание образов и многие другие[2].
Разработанная программа представляет собой простейший пример средства для анализа поведения клеточных автоматов. В настоящее время авторами разрабатывается CAMEL (Cellular Automata Modeling Environment & Library — среда моделирования и библиотека разработчика клеточных автоматов), которая предоставит развитый инструментарий для решения задач с применением клеточных автоматов различных типов.
Работа выполнена при поддержке Российского фонда фундаментальных исследований по гранту №02-07-90114 «Разработка технологий автоматного программирования».
Литература
- Наумов Л.А., Шалыто А.А. Клеточные автоматы. Реализация и эксперименты // Мир ПК. 2003. №8.
- Тоффоли Т., Марголус Н. Машины клеточных автоматов. М.: Мир, 1991.
- Троицкий Е. Цветовые модели // Программист. 2003. №1.
- Гордеев А.В., Молчанов А.Ю. Введение в системное программирование. СПб.: Питер, 2001.
- Мешков А.В., Тихомиров Ю.В. Visual C++ и MFC. СПб.: БХВ-Петербург, 2000.
- Гурский Д., Стрельченко Ю. Оптимистичный футуризм // Мир ПК. 2003. №1.
- Информатика. Энциклопедический словарь для начинающих. М.: Педагогика-пресс, 1994.
- Гарднер М. Крестики-нолики. М.: Мир, 1992.
Об авторах
Лев Александрович Наумов — студент кафедры «Компьютерные технологии» Санкт-Петербургского государственного института точной механики и оптики (технического университета) — СПГУ ИТМО. E-mail: levnaumov@mail.ru.
Анатолий Абрамович Шалыто — профессор кафедры «Компьютерные технологии» СПГУ ИТМО. E-mail: shalyto@mail.ifmo.ru http://is.ifmo.ru.
