Занимательное программирование
Почти четыре столетия назад Блез Паскаль заметил: «Предмет математики настолько серьезен, что нужно не упускать случая сделать его немного занимательным». То же самое справедливо и по отношению к программированию.
Игра в камешки и лестница Кутафьей башни
Давайте рассмотрим простую игру [1]. Имеется кучка из N камешков. Каждый из двух играющих по очереди может извлекать их из этой кучки, при этом он должен брать не менее одного и не более удвоенного числа камешков, взятых противником на предыдущем ходу. Вначале он может взять любое их число (но не все сразу). Выигрывает тот, кто берет последний камешек. Вопрос: какой должна быть стратегия, ведущая к победе? Уточним задачу: сколько камешков надо взять первому игроку, если начальное их число равно 1000?
С чего начать? Как подступиться к решению? Можно ли решить задачу в уме, придется ли воспользоваться калькулятором или нам даже потребуется построить вспомогательные устройства и механизмы? А вообще имеет ли эта задача решение? Если на такой вопрос можно ответить однозначно, то считайте, что полдела сделано. Упростим нашу работу. Эта задача имеет решение, притом в уме, и с помощью калькулятора вы вряд ли его найдете (еще одна подсказка: оно единственное). Решение задачи строится в форме алгоритма. Значит, нам просто нужно описать задачу на каком-нибудь языке программирования и, нажав кнопку, получить ответ? Не спешите. Далеко не всегда «лобовой» способ приводит к успеху.
Попробуем сначала разобраться в природе задачи и отыскать ключ. То, что играющие могут удваивать число камешков по отношению друг к другу, наталкивает на мысль, что здесь не обойтись без методов, построенных на степени числа 2. Однако как учесть, что количество извлекаемых из кучки камешков может быть любым (в пределах удвоенного числа, взятого противником)? Пока не догадались? Тогда рассмотрим другую, более простую задачу, а к первой еще вернемся.
Из Александровского сада к Кутафьей башне, служащей входом на Троицкий мост Московского Кремля, ведет небольшая лестница. Ее высота 4,5 м, а длина основания 13,5 м (эти стороны образуют катеты прямоугольного треугольника). Для формирования ступенек используются плиты высотой 30 см и шириной 50 см. Вопрос: сколькими способами можно построить лестницу? [2]
Сначала обратим внимание на то, что плиты можно располагать встык (в том числе и поднимать ровно на их высоту), но нельзя их класть друг на друга. Поскольку высота лестницы составляет 4,5 м, то всего у нас будет ровно 15 ступенек по 30 см высотой, а количество плит равно 27 (это ясно из размеров основания лестницы и ширины плиты). Теперь до того, как понять способ решения задачи (но не точного определения числа вариантов – оно достаточно велико), нам остался всего один шаг. Девиз корпорации IBM «Думай!» (Think) – весьма популярная шутка в мире программистов, но в данной ситуации он весьма актуален.
Отложим на время обе задачи и зададимся вопросом: а что же такое алгоритм? Самое простое определение звучит так: это набор инструкций, который описывает, как некоторое задание может быть выполнено. Алгоритм характеризуют пять признаков:
- вход (входные данные, предусловия);
- выход (выходные данные, постусловия);
- конечность (алгоритм должен заканчиваться после выполнения конечного числа шагов);
- определенность шагов (каждый шаг алгоритма должен быть точно определен);
- выполнимость шагов (возможность ручной проверки).
Последний признак является самым туманным. Наиболее удачное неформальное определение выполнимости принадлежит Дональду Кнуту и приведено в его знаменитом труде «Искусство программирования» [1]. Он говорит, что инструкция выполнима, если включенные в нее операции достаточно элементарны, чтобы их за конечное время мог выполнить человек, вооруженный карандашом и бумагой.
Процесс интуитивного увязывания условий задачи с теми или иными алгоритмами, пожалуй, ключевой и наиболее трудный момент в ее решении. Но даже после того, как нам дают подсказки и приводят идею-«отмычку», встает вопрос технической реализации – ведь необходимо получить конкретный ответ. В программировании, как и в математике, поиск «отмычки» ведется на интуитивном уровне путем сопоставления задачи с уже знакомыми путями решения. Техническая же сторона здесь выглядит по-иному.
Комбинаторика и треугольник Паскаля
Вернемся к задаче о лестнице Кутафьей башни. Попробуем ее упростить. Если каждую ступеньку обозначить через 1, а плиту через 0, то любой вариант лестницы будет последовательностью нулей и единиц длиной m + k, где m – количество плит (в нашем случае 27), а k – количество ступенек (у нас их 15). Причем единицы не могут стоять рядом друг с другом (ступеньки не могут громоздиться). Сначала выписываем 27 нулей. Для единиц у нас есть 28 мест. Теперь нам осталось ответить на такой вопрос: сколькими способами можно расставить 27 нулей и 15 единиц так, чтобы никакие две единицы не стояли рядом? Другими словами, как выбрать 15 из 28 мест. Вспомним комбинаторику. Там есть такие понятия, как перестановки (n!), размещения без повторений ( Ank= n! / (n-k)! ) и сочетания ( Cnk= n! / (k!x(n-k)!) ). Нас интересуют сочетания. Это и есть путь к решению. Но попробуйте подсчитать это число (C2815 = 37 442 160) в нашем случае. А если мы увеличим масштаб задачи? Итак, с технической точки зрения для задачи о лестнице Кутафьей башни нам нужно только построить специальную арифметическую машину, вычисляющую число сочетаний.
Как ее строить? Вычисление факториала – вроде бы довольно простая в реализации функция: последовательно уменьшай на единицу исходное число и все время перемножай с промежуточным результатом. Тут, правда, есть неприятная проблема: факториал растет так быстро, что уже 12! = 479 001 600, а поскольку представление целых чисел в современных ПК ограничено 32 разрядами, следующее значение выходит за разрядную сетку.
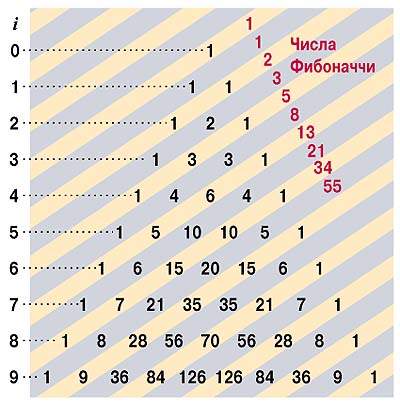 |
| Треугольник Паскаля |
Опять вспомним математику (куда же без нее?). Число сочетаний можно вычислять не через факториал, а с помощью арифметического треугольника. Взгляните на рис.1. Строится треугольник довольно просто: его бедра и вершина состоят из единиц, а в основании каждый элемент строки получается суммированием двух стоящих непосредственно над ним элементов.
Арифметический треугольник мы неизменно связываем с именем Паскаля. В 1653 г. Блез Паскаль опубликовал одну из самых своих известных работ – «Трактат об арифметическом треугольнике» (в нем треугольник был повернут: его ребра выполняли роль катетов). Этот треугольник был известен еще в Древней Индии (X в.), а в XVI в. вновь открыт Штифелем.
Несложно заметить особенности треугольника: он симметричен относительно вертикальной оси, проходящей через его вершину. Первые внутренние диагонали, параллельные бедрам треугольника, образуют ряд натуральных чисел. Суммы чисел, стоящих вдоль не круто падающих диагоналей (получаемых ходом коня), образуют последовательность Фибоначчи. Связь между треугольником Паскаля и числами Фибоначчи была обнаружена лишь в XIX в. Обратите внимание на следующие свойства чисел треугольника Паскаля:
- Сумма всех чисел каждого ряда равна соответствующей степени числа 2 (известное свойство биномиальных коэффициентов).
- Сумма чисел на любой диагонали равна числу, расположенному снизу и слева от последнего слагаемого, соответственно нё ni=1 i = Cn+12.
- Cnk = (n / k ) x Cn-1k-1 (внесение/вынесение).
- Cnk = Cnn-k (симметрия).
- Cnk = Cn-1k + Cn-1k-1 (сложение).
- Cnk = (-1)k x Ck-n-1k (обращение индекса).
- Cnm x Cmk = Cnk x Cn-km-k (упрощение произведений).
Известный популяризатор математики Мартин Гарднер [3] справедливо заметил, что «всякий раз, когда целые числа располагаются по какой-нибудь красивой единственно возможной схеме, у этой схемы оказывается масса самых неожиданных свойств». Свойства треугольника Паскаля поистине неисчерпаемы. Но пока нас все же будет интересовать его использование для нашей конкретной задачи.
Будем считать, что адресация элементов нашего треугольника записывается в виде: c(i,j), где i – номер строки (основания), а j – номер элемента на строке. Оба индекса нумеруются от 0. Самым важным для нас свойством треугольника Паскаля является то, что эти элементы и определяют число искомых сочетаний, т. е. c(i,j) = Ci j, они же являются биномиальными коэффициентами, используемыми при разложении (x+y)n в бином Ньютона. (Биномиальные коэффициенты были подробно описаны индийским математиком Бхаскара Ачарья еще в 1150 г.)
Теперь у нас есть два варианта:
- реализовывать треугольник в виде какого-нибудь алгоритма и затем (для возможности практического применения) пытаться построить к нему «подюездные» пути;
- сначала построить каркас, обеспечивающий «подюездные» пути, а затем наращивать его соответствующими алгоритмами.
Для программирования в малом обычно используют первый вариант, как более легкий, но мы выберем второй – он позволит лучше понять процесс конструирования. Процесс превращения алгоритма в программу Ахо, Хопкрофт и Ульман [4] называют его пошаговой кристаллизацией. Ею мы займемся сразу после построения каркаса.
Проект Triangle
Начнем с архитектуры. Основными строительными блоками для нас будут модули и процедуры, а не классы и методы (их мы также будем применять, но лишь там, где это действительно требуется). Причина прозаична: эйфория обюектно-ориентированного программирования (ООП) потихоньку уходит в небытие. Попытки решить все проблемы с помощью ООП уступают место прозрению: с наступлением компонентного программирования (component-based programming) меняется отношение к средствам инкапсуляции (предложенным еще Д.Парнасом в начале 1970-х годов), которые за последнее десятилетие были оттеснены классами на задний план. Речь идет о модулях.
С точки зрения области видимости и области существования между модулем и процедурой имеется существенная разница. Процедура прозрачна для импорта (все, что описано снаружи, автоматически видно и внутри нее) и закрыта для экспорта (за исключением списка формальных параметров). Модуль играет роль контейнера и вбирает в себя процедуры (а также классы, как специальные структуры данных со связанными процедурами) и устанавливает жесткие границы экспорта и импорта. Локальные элементы в процедурах существуют ровно то время, пока вызвана процедура, и уничтожаются после ее завершения. Локальные элементы в модулях существуют ровно то время, пока загружен модуль (как правило, до конца работы программы). Модули могут динамически подгружаться и выгружаться.
В качестве главной архитектурной схемы мы будем опираться на ставшую популярной благодаря языку Smalltalk концепцию MVC (Model/View/Controller , модель–вид–контроллер). Идея крайне проста: подобно тому как любая программа стоит на трех «китах» – на данных, логике и внешнем интерфейсе, в MVC они отображаются соответственно на модель, контроллер и вид. Предполагается, что модель обычно выступает в одном экземпляре, видов может быть много, а контроллер играет роль связующего слоя между первым и вторым.
Дополним и разовьем эту идею. По аналогии с концепцией MVC разобьем все наши модули на три вида:
- машины («системный» слой, модель);
- преобразователи (связующий слой, контроллер);
- сценарии («прикладной» слой, вид).
Преобразователи могут быть универсальными и специализированными. Универсальные имеют общий характер (привычные библиотечные модули); специализированные соединяют машины и сценарии. Деление на три вида совсем не обязательно должно предусматривать соответствие машин, скажем, уровню модели. Машина может использоваться и на уровне контроллера, если это удобно для данной задачи. Для иллюстрации наших решений мы будем использовать язык Оберон-2 [5].
В качестве примера программирования на этом языке приведем использование новой базовой идеи Оберона (www.osp.ru/studio, www.oberon.ethz.ch) и Оберона-2 [5] – концепции расширения типа. Она раскрывается в реализации вспомогательного библиотечного модуля Time (листинг 1). При тестировании и выявлении эффективности реализации алгоритмов нам потребуется его секундомер.
Арифметическая машина реализуется в виде модуля, у которого есть команды (процедуры без параметров, берущие данные из регистров и сохраняющие там результаты) и вспомогательные процедуры. Она имеет индикаторы состояния (булевы переменные, характеризующие текущее состояние), а также обязательные команды On (включение, инициализация) и Off (выключение, финализация). Взгляните на «печатную машинку» – простейшую машину TypeWriter для вывода на экран (листинг 2).
Сценарии подразумевают обработку информации на уровне текстовых строк. Посмотрим, как для нашей задачи реализуется сценарий (листинг 3). Он выполнен в виде компактного модуля Triangle (это будет наш головной модуль) и опирается на специальный преобразователь с именем TriangleTF, которому для удобства работы мы присвоим синоним TT.
При работе на каждом слое будем придерживаться следующего деления по видам представления данных:
- «регистровое» представление (поля записи);
- бинарное представление (бинарный вид);
- внешнее представление (строка).
Теперь на каждом из уровней определим поддерживаемые виды представления данных:
- машины – вход: «регистры»; выход: «регистры»;
- преобразователи – вход: бинарный вид, «регистры», строки; выход: бинарный вид, «регистры», строки;
- сценарии – вход: строки; выход: строки.
Проект Triangle. Структура модулей
| Уровень | Модуль | Назначение |
| RTS | ||
| In | Ввод | |
| Out | Вывод | |
| Library | ||
| Str | Обработка строк | |
| CharSet | Множества литер | |
| Number | Форматирование чисел | |
| Time | Часы и секундомер | |
| Math | Математические функции | |
| Parsing | Разбор строк | |
| TypeWriter | Машина вывода на экран | |
| TriangleTst | Тестирование | |
| Model | ||
| Pascaline | Абстрактная машина | |
| Controller | ||
| TriangleTF | Преобразователь | |
| View | ||
| Triangle | Сценарий, головной модуль | |
Посмотрим, какой в итоге будет структура модулей нашего проекта (см. таблицу). Наибольший интерес в реализации для нас представляет модуль Pascaline, содержащий основные алгоритмы исходной задачи и созданный по аналогии с «паскалиной». При проектировании этого модуля будем исходить из того, что нам потребуется реализовывать несколько вариантов алгоритма (для их сравнения). При этом понадобится переключатель, который обеспечивал бы настройку команды машины на соответствующую процедуру, реализующую данный алгоритм (в нашем случае это семейство процедур PascalTriangle и Fibonacci, реализованные через процедурные типы). Интерфейс модуля Pascaline представлен на листинге 4. Основные структуры данных модуля Pascaline можно видеть на листинге 5.
Итак, каркас у нас практически готов, осталось только реализовать алгоритмы и написать связующий модуль TriangleTF.
Продолжение в следующем номере.
Литература
1. Кнут Д. Искусство программирования, т.1. М.: Вильямс, 2000.
2. Виленкин Н.Я. Популярная комбинаторика. М.: Наука, 1975.
3. Гарднер М. Математические новеллы. М.: Мир, 2000.
4. Ахо А., Хопкрофт Дж., Ульман Дж. Структуры данных и алгоритмы. М.: Вильямс, 2000.
5. Moessenboeck H. Object-Oriented Programming in Oberon-2. Springer, 1993.
6. Гиндикин С.Г. Рассказы о физиках и математиках. М.: МЦНМО, 2001.
Алгоритм
Как это ни странно, слово «алгоритм» возникло от имени автора знаменитого персидского учебника по математике аль-Хорезми. Именно в его изложении десятичная система счисления индусов после перевода на латынь и выпуска книги Леонардо Пизано (Фибоначчи) стала доступна европейцам. Интересно, что гордостью коллекции Дональда Кнута является гашеная почтовая марка с изображением аль-Хорезми, выпущенная в 1983 г. в СССР к 1200-летию ученого и просветителя Востока.
Блез Паскаль и «паскалина»
Блез Паскаль (1623б-1662) – один из самых знаменитых людей в истории человечества [6]. В 1640 г., чтобы помочь своему отцу, Этьену Паскалю, Блез придумывает машину, позднее названную Pascaline – «паскалина». Основная идея ее работы – каждое колесо (всего их восемь), совершая движение на десять цифр, заставляет двигаться соседнее колесо ровно на одну. Машина производила четыре действия над пятизначными цифрами. По чертежам Паскаля было изготовлено около 50 экземпляров. Относительно недавно стало известно, что Шиккард, друг Кеплера, в год рождения Паскаля построил другую арифметическую машину, однако машина Паскаля была куда совершеннее. «Это приспособление, – вспоминает сестра Блеза, Жильберта Перье, – рассматривали как новшество в природе, сводившее к совокупности машинных действий то знание, которое всегда было закреплено за умом».
Языки Оберон и Оберон-2
Язык Оберон (Oberon) был создан Никлаусом Виртом в 1988 г. при активном участии фрга Гуткнехта. Он стал дальнейшим развитием линии языков Паскаль (1970) – Модула-2 (1979). Оберон – это король эльфов и муж Титании (Titania), ставший персонажем известного произведения Вильяма Шекспира «Сон в летнюю ночь». Именем Оберон был назван самый дальний и второй по величине спутник планеты Уран, открытый Уильямом Гершелем в 1787 г. Никлаус Вирт решил дать название «Оберон» языку, системе и специальному проекту под впечатлением успешного полета американского корабля Voyager 2 (из серии NASA Mariner), который, стартовав осенью 1977 г. (в год проектирования языка Модула-2), к январю 1986 г. достиг Урана. Язык Оберон-2 (1991) явился небольшой ревизией Оберона (добавлены открытые массивы, связанные процедуры, ограничение экспорта, оператор FOR). Два языка развиваются независимо и подобно ОС UNIX формируют целое дерево разных диалектов (www.oberon.ethz.ch/genealsys.html).
