В № 6 "Мира ПК" за 1998 г. была опубликована работа В. Любченко "Новые песни о главном". Настоящая статья является попыткой подпеть автору "новых песен" речитативом. Замечу сразу, что идеи В. Любченко очень интересны, хотя и не бесспорны.

Итак, все должно начинаться с основного вопроса: какой математический аппарат нужно выбрать, чтобы решить поставленную задачу. В связи с этим весьма важно рассмотреть два основных направления, существующие в настоящее время. Первое, теоретико-множественное (переборное) основывается на теории множеств и конечных автоматов. Второе, конструктивно-алгоритмическое опирается на теорию рекурсивных функций и машин Тьюринга.

Чтобы решить задачу теоретико-множественным путем, нужно разработать конечный автомат, а значит, перебрать и проанализировать формально описывающие его множества:

  • множество комбинаций сигналов на входе и выходе;
  • множество состояний;
  • множество соответствий переходов и выходов.

Иначе говоря, разработчик надежного автоматического устройства должен заранее перебрать и запрограммировать все возможные в процессе управления ситуации и заложить в его память адекватные действия, которые следует выполнять при возникновении каждой из ситуаций.

Чтобы решить задачу конструктивно-алгоритмически нужно построить такую машину Тьюринга, которая вычислит решение, обрабатывая любую входную ситуацию единообразным алгоритмом, подчиненным минимаксной стратегии управления1, не имея заранее сформированного множества ситуаций и ответов на них.

Первое направление очень трудоемко. Кроме того, теоретико-множественный подход дает экспоненциальное (ax, где а - число состояний объекта, х - число объектов) усложнение задачи и при незначительном росте числа объектов, которыми управляют, приводит к так называемому комбинаторному взрыву. Например, число состояний объектов - 2 (включен, выключен), число объектов - 10 (выключатели, клапаны и т. п.), следовательно, число состояний системы 210=1024. При увеличении числа объектов всего на 5, число состояний системы увеличится ни много ни мало на 31 744 и составит 215=32 768.

Все эти состояния придется перебирать разработчику. Сам перебор, конечно, может выполнить и ЭВМ, однако для каждой из полученных на ЭВМ комбинаций нужно будет установить однозначное соответствие по принципу "если... то...", а это уже придется делать вручную. Предположим, что задачей занимается супер-разработчик, который тратит на анализ ситуации в среднем одну минуту. Тогда но то, чтобы проанализировать все ситуации, ему потребуется 32 768/60=546 часов непрерывной работы - а ведь в системе всего-то 15 выключателей! И что будет, если он где-то ошибется?

В противовес автомату, конструктивно-алгоритмический подход дает полиномиальную (а*х) сложность решения задачи, и при увеличении числа объектов увеличится лишь число итераций цикла.

Чтобы наглядно представить эффективность конструктивно-алгоритмического подхода, рассмотрим следующий пример.


Рис. 1

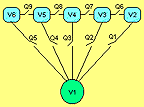На рис. 1 показана сеть, которой нужно управлять.

Здесь V1 - сервер, V2-V6 - клиенты, Q1-Q9 - выключатели сетевых линий. По линиям передается информация или энергия. Сеть подвержена внешним воздействиям, в результате которых в любом ее месте может возникнуть разрыв связи. Требуется управлять сетью так, чтобы обеспечить ее живучесть, т. е. то или иное соединение всех клиентов с сервером при различных отказах линий. Приступим к формализации задачи.


Рис. 2
Для создания конечного автомата нужно запастись памятью, перебрать 29=512 ситуаций, создать базу ситуаций, базу адекватных реакций на них и поисковую машину. Решая ту же задачу конструктивно, нужно найти такую рекурсивную функцию, которая бы строила минимаксные деревья. Рассмотрим это решение.

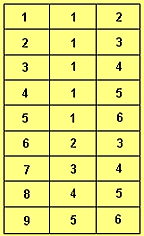Сеть моделируется графом (рис. 2), где вершина 1 представляет сервер, вершины 2-6 - клиентов, а ребра 1-9 - линии сети. Номера ребер соответствуют их приоритетам. Процесс управления сводится к построению связанных деревьев (графов без циклов) с максимальной пропускной способностью. Представим модель сети в памяти ЭВМ в виде укороченной матрицы смежности, где в первом столбце находятся номера ребер, а во втором и третьем - номера смежных вершин.

В 1956 г. Дж. Краскалом был предложен алгоритм получения минимального дерева. Следуя ему, нужно последовательно просматривать ребра в соответствии с приоритетом, и, если текущее ребро не образует цикла, добавлять его в структуру, а в противном случае переходить к следующему ребру.


Рис. 3

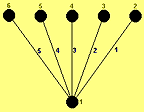Рассмотрим теперь процедуру управления структурой на следующем примере. Пусть в исходной структуре, показанной на рис. 3, произошел обрыв связи N 5 (ребро 5).

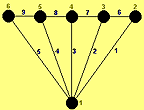
Обнуляем пятую строку массива и строим новую структуру. На очередном шаге построения нового дерева добавляем очередное ребро (ребро 6) и запускаем процедуру поиска циклов. В данном случае цикл есть, ребро включать не надо. То же самое происходит с ребрами 7, 8, и только ребро 9 будет включено как не образующее цикла (рис. 4). Итеративная процедура на этом заканчивается по условию достижимости отключенной вершины 6.


Рис. 4
Чтобы алгоритм не зацикливался в случае полной потери связи с какой-либо вершиной, все инцидентные ей ребра обнуляются и она не рассматривается. Здесь предлагается лишь концепция применения рекурсивной процедуры взамен переборной, и, чтобы не утомлять читателя, вопросы, связанные еще и с техническим состоянием линий (исправна, неисправна), опускаются.

И наконец, перейдем к выводам.

Какой же математический аппарат нужно выбрать?

  1. С помомщью конечного автомата эффективно моделировать системы, число состояний которых мало (на практике не более 8).
  2. Автоматную таблицу нужно обязательно строить на стадии формализации технического задания для решения проблемы определения полноты и непротиворечивости.
  3. Переборный метод является единственным при решении задач методом "тыка" (например, при подборе ключа).

Конструктивно-алгоритмический аппарат нужно использовать при разработке алгоритмов управления системами, число состояний которых велико, и для обеспечения управляющей системе алгоритмической надежности.

Дело в том, что, создавая конечный автомат для управления большой системой, разработчик просто физически не сможет проанализировать все ситуации, а значит, вынужден будет пропускать так называемые "редкие события" и не заносить их в память ЭВМ. Поэтому если такое событие происходит (вспомним чеховское ружье), то конечный автомат дает сбой. Конструктивный же алгоритм всегда вычислит правильный ответ на любую заранее не заданную разработчиком ситуацию, обеспечивая тем самым алгоритмическую надежность управления.

И еще. К сожалению, не существует математического аппарата, пригодного на все случаи жизни. И при выборе нужно руководствоваться, во-первых, тем, какие задачи решает разработчик, а во-вторых, тем, какой тип структурного решения ему подскажет интуиция. Но это тема уже других песен.

1Стратегия управления, при которой минимизируется максимальная (из всех возможных) опасность. Другими словами, при любом отказе нужно управлять так, чтобы последствия отказа были минимальны.