Концепция эволюции

Путь к построению высокопроизводительной аппаратуры

Путь к радикальному увеличению производительности и сложности компьютерной аппаратуры подсказывает концепция эволюции, изложенная в трудах Анри Бергсона. Она не получала развития, поскольку не был найден способ объективизации длительности. Между тем, разделение задач на вычислительные и на задачи взаимодействия (или на синхронные и асинхронные задачи) со своей схемотехникой открывает такую возможность.

Рассматривая вопрос о перспективах развития компьютерной аппаратуры, в первую очередь имеют в виду возможность увеличения сложности и быстродействия. Встает вопрос об ограничивающих факторах. Если говорить о технологии, то в качестве ограничителя на первом месте всегда был предел возможного уменьшения ширины проводника или (что то же самое) увеличения тактовой частоты. Но наряду с этим все большее значение приобретает второй ограничительный фактор, связанный с архитектурой, — фактор цепей синхронизации.

Лучше всего это проследить на примере процессоров. Синхронизация выглядит незначительной деталью в вопросе организации совместной работы узлов процессора, однако по мере увеличения сложности ее реализация требует все больше усилий от разработчиков, а по мере совершенствования архитектуры процессоров превращается в главный фактор ограничения производительности. На практике получается, что для обеспечения синхронизации необходимо создавать чрезмерно сложный механизм управления [1].

В чем же тут дело? Синхронизация — не просто некоторое удобство, позволяющее обеспечить правильное срабатывание цепи. В этом техническом приеме как в зеркале находит отражение ключевой принцип современной науки — ориентация на измерение в определенных точках времени.

Для разъяснения этого вопроса придется обратиться к философии, исследующей свойства науки как системы познания реального. Сам по себе научный подход создавался в течение длительного периода и был разработан по вполне определенному сценарию, сформулированному в трудах Платона и Аристотеля. Эйнштейн как физик и философ, опираясь в основном на теорию множеств Кантора, настаивал на том, что эта система познания является единственной как для описания, так и для практической работы в реальности. Его главными оппонентами еще в ту пору были физик Бор и философ Бергсон, считавшие, что содержание реальности не исчерпывается каким-либо одним теоретическим языком. На идеи Бергсона мы и хотим обратить особое внимание [2].

На основе простых и ясных наблюдений он делает вывод, что наука по отношению к природе действует подобно кинематографической съемке: она останавливает время и производит замер состояния природы, фиксируя тем самым объект наблюдения. Чтобы воспроизвести движение, съемка многократно повторяется, но все равно время преобразуется в последовательность точек, возможно очень густо поставленных. Именно этот прием и открывает путь к использованию счета, к измерению, когда время является дискретным и выступает в роли независимой переменной, а объекты определяются своим положением в пространстве, т. е. по величине амплитуды. Этот способ объективизации непосредственно воспроизводится в аппаратуре цепями синхронизации, разбивающими время на последовательные такты. Поэтому архитектура современной компьютерной аппаратуры — это архитектура формирования состояний и переходов из одного состояния в другое.

Бергсон показывает, что наука не может охватить природу целиком, так как физические законы отражают только количественные отношения между объектами. Наука не понимает жизни. Движение заключает в себе нечто большее, чем последовательные положения, приписываемые подвижному телу наукой, это то, что называется становлением или эволюцией. Природа не измеряет и не считает, она длится, поэтому объективно существует второй способ познания, основанный на непрерывном потоке времени. Этот способ, повсеместный в природе, составляет содержание интуитивного начала. Исследуя свойства интуитивного, Бергсон показывает, что оно реализуется в природе методами организации и осуществляется на практике в виде последовательности событий, а не состояний. В области эволюции время существует как длительность, оно реально и играет ключевую роль, оно само существо эволюции.

Если изложить идеи Бергсона применительно к компьютерной аппаратуре, можно выделить два ее вида: это привычная аппаратура, работающая в дискретном времени, и аппаратура организационного плана, обеспечивающая решение задач взаимодействия, согласования работы отдельных систем, а не вычисления. Аппаратура второго типа должна функционировать в режиме непрерывного изменения входных сигналов, т. е. в режиме асинхронной передачи.

Может быть, это фантазия философа? Нет, в природе таких примеров масса. Этот принцип используется повсеместно в биологических системах. Давайте послушаем самого Бергсона. «Две вещи одинаково поражают в таком органе, как глаз: сложность структуры и простота функционирования. Глаз состоит из различных частей: склеры, роговой оболочки, сетчатки, хрусталика и так далее. Каждая из этих частей делится до бесконечности. Возьмем хотя бы сетчатку. Известно, что она состоит из трех слоев нервных элементов, расположенных один на другом: клетки мультиполярные, клетки биполярные, клетки зрительные; каждый слой имеет свою индивидуальность и представляет, без сомнения, очень сложный организм: и это еще очень упрощенная схема тонкой структуры этой оболочки. Такой аппарат, как глаз, состоит, следовательно, из бесконечного числа аппаратов, каждый из которых чрезвычайно сложен».

Выработанная природой система взаимодействия этих аппаратов не только эффективна и надежна: «Как только глаз открывается, осуществляется видение».

Итак, анализ природных систем показывает, что высокопроизводительная компьютерная аппаратура должна включать системы двух видов: вычислительные синхронные и организующие асинхронные, потоковые. Эта комбинация и есть тот отработанный природой способ, который указывает направление для создания сверхсложных и сверхэффективных систем. Уместно и следующее сравнение: в вычислительных системах координирующие функции «омертвлены» в виде цепей синхронизации, а в потоковых системах они — сама суть аппаратуры.

Все эти идеи были сформулированы приблизительно сто лет назад, но так и остались невостребованными, поскольку никто не смог предложить способа работы с длительностью. Теперь ситуация изменилась, но для этого потребовались радикальные предложения. Дело в том, что философия Бергсона отвечает принципу дополнительности и потому предполагает построение второй системы знания — абсолютно самостоятельной и полярной как в основах, так и в моделях представления по отношению к науке.

Такая работа в определенной степени была проделана, а ее результаты изложены в [3]. Когда в физике говорят о взаимодействии, то понимают его как сигнал, поэтому проделанная работа прежде всего касается изменения модели сигнала.

Модель сигнала, выработанная наукой и используемая во всех областях техники, настолько привычна для нашего восприятия, что кажется само собой разумеющейся. Вот она: для представления сигнала используется траектория, т. е. линия, образованная множеством точек значений амплитуды, от которой можно перейти к функции и к применению функционального анализа.

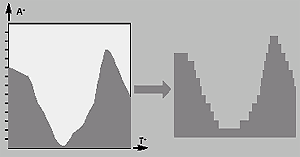
Эта модель должна быть отменена. Вместо этого для представления сигнала можно применить область, которая является частью плоскости. После ее разбиения на слои в горизонтальном направлении возникают непрерывные интервалы времени, а сам сигнал превращается в симплициальный комплекс или, что то же самое, разбивается на множество последовательностей прямоугольных импульсов, расположенных друг над другом в пространстве (см. рис. 1). При продвижении к вершине сигнала длина симплекса убывает, а длина промежутка симплекса увеличивается при постоянстве величины периода, поэтому симплициальный комплекс обеспечивает воспроизведение формы сигнала, как это и показано на рисунке. В отличие от общепринятого представления, прямоугольные импульсы — тоже области, а не линии траекторий, ограничивающие их форму. Такое разложение получается при квантовании сигнала по уровню.

Рис. 1. Представление сигналов интервалами

Переход к областям означает полный отказ от математики и переход на двоичную логику, которая по определению не включает условий завершения выполнения своей задачи, т. е. допускает непрерывную длительность. Сигнал в этой модели подобен потоку, состоящему из отдельных струй. Преобразования сигнала выполняются не путем изменения величины вектора мгновенного значения амплитуды, а совсем на иной основе. Такими преобразованиями могут быть, например, изменение длины интервалов симплексов, изменение числа уровней квантования, занимаемых группой симплексов, изменение порядка следования симплексов по уровням квантования и т.д. Технология преобразования в потоке для более сложных случаев предусматривает применение признаков качественного описания, обеспечивающих не вычисление, а узнавание при работе с сигналами. Все эти возможные процессы являются алгоритмическими по своей сути и их применение превращает координирующие цепи в интеллектуальные, а не просто соединяющие.

Посмотрим, как это реализуется в случае задачи сложения двух сигналов, когда они оказываются в одном потоке [4].

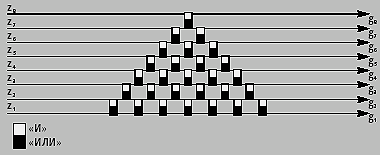
Рис. 2. Сумматор для сигналов, представленных интервалами

Схема сумматора приведена на рис. 2. Входные шины Z сумматора соответствуют уровням квантования для всей области представления сигнала, поэтому прямоугольные импульсы симплексов поступают на сумматор по этим входам. Схема построена так, что в ней обеспечивается вычисление локальных максимумов и минимумов во всех точках логического связывания между собой входных шин Z. Все, что делается в схеме, так организуется движение симплексов в поперечном по отношению к потоку времени направлении, в данном случае сверху вниз. Благодаря этому все импульсы на выходах сумматора выстраиваются плотно, по порядку снизу вверх, когда более длинные оказываются внизу.

В случае двух сигналов число входных шин сумматора должно быть достаточным для подключения этих сигналов, при этом симплексы сигналов могут произвольным образом распределяться по входным шинам. Независимо от этого на выходных шинах формируется симплициальный комплекс, соответствующий сигналу суммы. На первом этапе движения происходит перемещение симплексов к нижнему краю схемы. На последнем этапе, когда происходит соприкосновение симплексов, начинается сортировка симплексов, в результате которой более короткие симплексы располагаются выше более длинных.

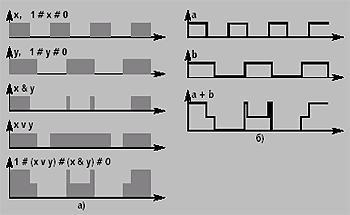
Рис. 3. Сложение двух последовательностей импульсов: а) представление с помощью области; б) представление с помощью линии

Если в обычном сумматоре сложение выполняется путем арифметического суммирования мгновенных значений амплитуд, то здесь — путем «укладывания» симплексов. Пример рис. 3 демонстрирует эту же процедуру на простом примере сложения двух последовательностей импульсов, показывая, какими аналитическими средствами и как можно ее описать. На рис. 3б импульсы, как обычно, представлены линиями, сумма здесь равна (a + b). На рис. 3а те же импульсы представлены областями. Подходящей аналитической записью для такого импульса является следующее логическое выражение (1# X # 0). В этом выражении текущий симплекс Х записан вместе с двумя сопровождающими его симплексами, один из которых располагается непосредственно выше (равен тождественно нулю), а другой непосредственно ниже текущего (равен тождественно единице), где знак # обозначает следование на соседних уровнях. Между симплексами двух сигналов сначала выполняются логические операции «И» и «ИЛИ» (знаки & и v), а затем результаты размещаются один над другим строго в той же последовательности, в которой перечислены эти логические операции (нижняя часть рис. 3а). Логическое выражение для суммы здесь такое (1# XvY # X&Y # 0). Как видно из примера, результат сложения один и тот же, хотя способы вычисления различны.

В обычном сумматоре действуют законы математики, требующие развертывания процесса выполнения во времени. Поэтому после каждого такта поступления входных сигналов следует такт удержания входных сигналов на время действия цепей переноса. Связь между источниками входных сигналов и сумматором на это время прерывается. В потоковом сумматоре связь между входами, выходами и источниками сигналов поддерживается постоянно, поэтому быстродействие здесь значительно выше.

Современная аппаратура, в том числе, и процессоры, совмещает и измерительные и потоковые задачи, но решаются они единообразно, что и вызывает трудности при увеличении сложности. Можно, конечно, пытаться синхронную реализацию менять на асинхронную или наоборот. В некоторых случаях это может привести к улучшению, но не более того. Мы же говорим о том, что в аппаратуре необходимо разделить все задачи на задачи вычисления и задачи взаимодействия, применяя к ним адекватные схемотехнические решения, и тогда откроются практически неограниченные возможности по созданию высокопроизводительной и сверхсложной аппаратуры.

Правда и об этом сейчас говорить еще рано, поскольку до этого должна быть создана схемотехника потоковых систем, которая находится в зачаточном состоянии. Потребуется определенное время, чтобы понять до конца ее перспективы и в еще большей степени — перспективы объединения двух направлений. Для этого нужны совершенно новые проекты, которые смогут гармонизировать эти направления. Но это можно делать не на пустом месте, ориентиром здесь является сама природа.

Применение потоковых систем, решающих задачи обеспечения взаимодействия, открывает новые горизонты в освоении реальности, открывает путь к системам, сложность и, одновременно, совершенство которых поразительны.

Литература

[1] Черняк Л. Вторая жизнь асинхронных процессоров. // Открытые системы, 2002, № 5

[2] Бергсон А. Творческая эволюция. Терра, 2000

[3] Ханджян О. Основы и начала теории представления. http://hark.narod.ru/book.pdf

[4] Ханджян О. Патент РФ № 1109888