Современные микропроцессоры общего назначения, как и различные специализированные процессоры, состоят из большого числа компонентов. Интегрирование этих компонентов в одном кристалле приводит к созданию так называемых «сверхбольших интегральных схем». Структурная и функциональная сложность таких систем весьма внушительна – миллионы логических вентилей, функции сотен и тысяч переменных; так, функциональные логические схемы «средних» периферийных устройств включают до 50 тыс. вентилей. Это делает актуальной задачу верификации, т.е. подтверждения того, что описание проекта, по которому микросхема будет реализована «в кремнии», полностью соответствует спецификации (техническому заданию) проектируемой системы.
Отмеченная сложность проектируемых систем означает невозможность «ручного» анализа правильности результатов разработки и указывает на то, что процедура верификации может быть очень длительной. Между тем, в современной электронной промышленности отрезок времени от начала разработки до выхода на рынок – один из наиболее критичных экономических показателей. Задержка с выходом на рынок на несколько месяцев из-за необходимости устранять ошибки может очень дорого обойтись компании-разработчику [1].
В качестве примера можно указать те неприятности, с которыми столкнулась Intel, не обнаружив вовремя некорректность выполнения деления с плавающей точкой в процессоре Pentium. В итоге потери корпорации составили 500 млн. долл. [2].
Как описываются требования к сложной цифровой системе
Трудности возникают уже в связи со спецификацией проекта. Скажем, как описать все многообразие требований к процессору изображений? Без этого, разумеется, ни о какой верификации говорить не приходится. Поэтому начнем наш рассказ с краткого анализа проблемы спецификации цифровых вычислительных систем, понимая вместе с тем, что это самостоятельная тема, способная занять не один десяток журнальных страниц.
Содержательно, под спецификацией проекта понимают по возможности сжатое описание всех значимых аспектов поведения системы, например, с целью проверки того, что они не противоречат некоторому набору исходных требований. Это может быть описание в форме требований к характеристикам функционирования или к функциональному составу и условиям реализации. Подчеркнем, что говоря о спецификации, мы подразумеваем функциональные и поведенческие, а не конструктивные и физические аспекты (скажем, требования к электробезопасности).
Для процессоров – как общего назначения, так и специализированных – это могут быть требования к конвейеризации (число выбираемых инструкций в одном машинном цикле), к размерам физического и виртуального адреса, размеру шины, быстродействию обмена по шине определенного интерфейса (скажем, поддержка 64-разрядной 33-мегагерцевой шины PCI), длительности машинного цикла и т.д.
Для того чтобы снять неоднозначность, в современной практике проектирования цифровых систем и в соответствующих САПР предусмотрены средства задания «уровня» описания, под которым понимается степень абстрагирования от технической реализации. Так, описание системы в терминах алгоритма (набора алгоритмов) работы системы (например, быстрое преобразование Фурье и протокол обмена данными и командами для сигнального процессора) может быть принято за верхний уровень, а транзисторная схема – за нижний.
Как правило, спецификации проекта в основном соответствуют иерархии процесса проектирования: начальному (более раннему) этапу проектирования отвечает более высокий (а, следовательно, более абстрактный) уровень спецификации.
Заметим, что с точки зрения программиста, язык описания конкретной предметной области (скажем, AutoLisp), соответствует более высокому уровню, чем любой универсальный алгоритмический язык программирования. Напротив, с точки зрения разработчика аппаратуры, любое описание без деталей реализации (например, описание поведения системы на C++) считается более высокоуровневым по сравнению с описанием на языке, позволяющем представление системы в терминах ее функциональных компонентов, например на языке VHDL.
Вообще же говоря, определение того, что находится на «верхнем» уровне описания, зависит во многом от решаемых задач и манеры проектирования.
На начальном этапе разработки представлением системы служит некоторый набор концепций («идей»), сформулированных в терминах той или иной модели. Можно избрать такую организацию процесса проектирования, при которой за исходную точку принимают алгоритм в терминах соответствующей теории. В таком случае спецификация может представлять собой описание алгоритма, который должен быть реализован проектируемым устройством. Например, его работа может быть описана как решение уравнения F(x)=0 на множестве действительных чисел; тогда на данном этапе проектное решение может состоять в выборе того, какой алгоритм следует реализовать, скажем, алгоритм Ньютона-Рафсона или Гаусса-Зейделя.
В других подходах алгоритм должен быть получен по некоторому «поведенческому» описанию целевой системы. С подобной поведенческой точки зрения определение «верхнего» уровня часто соответствует описанию поведения системы (например, на уровне входов-выходов) до какой-либо декомпозиции на блоки и даже до определения того, какую часть функций следует реализовать программными, а какую – аппаратными средствами.
Этапы проектирования и разработки
Собственно проектирование целевого устройства как цифровой вычислительной системы начинается тогда, когда конструктор приступает к описанию поведения («поведенческой модели») проектируемой системы, специфицируя множество операций, требования к последовательности выполнения и размещения, временным характеристикам, а также задает условия отсутствия различных нерабочих состояний системы, например, системного тупика (deadlock). На этом же этапе принимаются основные решения о составе функциональных блоков (АЛУ, регистры, уровни кэширования и т.д.).
|
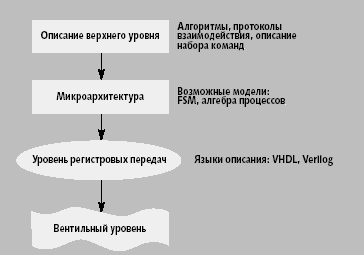
| Рис. 1. Уровни логической спецификации цифровых вычислительных систем |
В современных САПР этот этап – «верхний» (рис. 1). Все дело в том, в каких терминах описывать «поведение». Для специализированных процессоров это описание может быть выполнено в терминах некоторых «абстрактных» общематематических операций (сложение, умножение, сдвиг), описывающих алгоритм работы проектируемого устройства. Для процессоров общего назначения как правило используют спецификацию набора команд (instruction set specification), которая по сути должна совпадать с содержанием такого документа, как Programmer's Reference, обычно создаваемого параллельно с процессором и описывающего результаты каждой из команд в терминах состояний регистров и участков памяти [3].
На следующем уровне под «поведенческим» обычно понимают описание микроархитектуры (соответствует информации из Hardware Reference, если говорить о процессорах общего применения). В частности, на этом уровне решаются такие задачи, как организация конвейера команд. В современных микропроцессорах, например, Alpha, выделяют от 50 до 200 компонентов микроархитектуры, которые проектируются самостоятельными группами разработчиков [4].
На этих стадиях поведение на отдельных системных циклах не рассматривается. В соответствующей спецификации никак не представлены способы технической реализации системы; она не зависит от того, по какой технологии система будет производиться (скажем, будет ли система в конце концов реализована на полузаказной логике или на базе FPGA). Следующая абстракция для спецификации вычислительных систем обычно соответствует так называемому уровню регистровых передач (register transfer level – RTL). Проектируемая система на этом уровне представляется как множество функциональных элементов (АЛУ, регистры, массивы памяти и т.д.).
С поведенческой точки зрения RTL позволяет моделировать поведение проектируемой системы по циклам внешней шины. Стоит упомянуть также близкий к RTL уровень арифметических операций, а также уровень анализа отдельных бит [5, 6].
Следующий уровень представления системы – вентильный, специфицирующий систему как сеть вентилей и триггеров. По сути, это «технологический» уровень: необходимые вентили обычно существуют как элементы «кремниевой» библиотеки, из которых с учетом критериев оптимизации по геометрическому обюему, быстродействию, потреблению энергии, контролепригодности и синтезируется система.
За вентильным обычно следует транзисторный уровень представления. В данном случае адекватной математической моделью являются не логические уравнения и не отношения (немного подробнее об этом говорится ниже), а системы дифференциальных уравнений, описывающие изменения обюемных электрических зарядов в транзисторных переходах. Автоматизированное проектирование в этом случае обладает существенной спецификой; поэтому все вопросы, включая верификацию, рассматриваются отдельно от САПР «логического» уровня. То же самое можно сказать об уровне компоновки, или, как еще говорят, «топологии» кристалла (layout), на котором основными математическими инструментами являются различные методы поиска путей на графах.
Разумеется, говоря о способе спецификации, используемом в конкретной системе автоматизированного проектирования, мы подразумеваем наличие некоторого языка ее представления. Действительно, должны существовать (и существуют) языки спецификаций разного уровня, соответствующие той или иной модели поведения. Семантика любого из языков базируется на некоторой модели того «мира», для выражения которого он предназначен. В частности, поскольку мы рассматриваем проектирование цифрового вычислительного устройства, для представления самого верхнего уровня может понадобиться «модель вычисления», т.е. более или менее формальное описание того, что понимается под словом «вычисление». С практической точки зрения это означает необходимость как-то задать структуру вычислений, которую впоследствии можно было бы интерпретировать в терминах элементов устройства или протекающих в нем процессов. Очень часто вычисления представляются моделью «машины конечного множества состояний» (finite state machine – FSM). Состояния машины моделируют «конфигурации» физических состояний функциональных элементов проектируемой системы. Физические же состояния выражают, например, в терминах «высокого», «низкого» или высокоимпедансного состояний внешних линий, кодов режимов (скажем, типы арифметических операций) и т.д. В данном случае мы имеем дело с микроархитектурным уровнем представления проектируемой системы. Описание состояний и переходов между ними, а также входных сигналов, обеспечивающих данные состояния и переходы, равно как и желаемые выходы и представляет собой описание FSM. Например, если разрабатывается контроллер светофора на перекрестке двух путей, то его выходы должны соответствовать цветам светофора. Представим их парой (c1, c2), где переменные c1 и c2 соответствуют цветам светофора на каждом из направлений – красному, желтому и зеленому. Однако из всех возможных комбинаций, допустимыми являются только четыре: (c1 = зеленый, c2 = красный), (c1 = желтый, c2 = красный), (c1 = желтый, c2 = красный) (c1 = красный, c2 = зеленый). В терминах переменных c1 и c2 могут специфицироваться входы, состояния и выходы.
Очень часто на этапе проектирования, использующем FSM-модель, конструктор располагает некоторым соединением основных структурных компонентов проектируемой системы (АЛУ, регистры, конвейерные элементы, контроллеры, порты и т.п.) – но без каких-либо «технологических» подробностей. Могут также использоваться средства САПР, позволяющие отобразить FSM-алгоритм в подобные компоненты, или построить требуемую схему в результате композиции FSM-моделей указанных компонентов [7].
FSM-представления лежат в основе подсистем моделирования различных САПР: Synopsis, Cadence, Polis, Mentor Graphic и др.
В качестве модели вычислений часто используется формализм «алгебры процессов» [8], или сетей Петри (в частности, временных сетей Петри) [9], особенно, если система разрабатывается как программно-аппаратная. Дело в том, что FSM-модель, как правило, предполагает синхронное взаимодействие компонентов системы. Однако это имеет место далеко не всегда, особенно для так называемых «встроенных» вычислительных систем, предназначенных для управления различными прикладными системами (например, автомобилем), и вынужденных взаимодействовать с большим числом неоднородных (по быстродействию, протоколам управления исполнительными механизмами и т.д.) компонентов.
Указанные формализмы позволяют представить совместно протекающие процессы, при необходимости определить некоторый порядок их выполнения, что позволяет описывать системы с асинхронно взаимодействующими компонентами. На них базируется семантика многих языков моделирования – CSP (Communicating Sequential Processes), CCS (Calculus of Communicating Systems) [8], PEPA (Performance Evaluation Process Algebra) [10].
Весьма характерный пример описан в [11], где показывается, как представленное на английском языке (разумеется, весьма ограниченном, по сути – псевдокоде) описание некоторого коммуникационного протокола транслируют в спецификацию алгебры процессов, представленную на языке PROMELA компании Bell Laboratories.
Существенно, что рассмотренное многоуровневое проектирование, в котором результат более высокого уровня служит спецификацией и «формализованным» заданием на синтез для последующего уровня (его стараются выполнить как можно более автоматизированным образом), представляет собой итеративный процесс. Приближение к оптимальной по тем или иным критериям системе выполняется путем анализа и коррекции полученных решений на каждом из уровней проектирования.
Современные языки описания аппаратуры (hardware description language – HDL) позволяют описывать цифровые системы на разных уровнях абстракции. Например, VERILOG и VHDL [6] позволяют моделировать на поведенческом, RTL и вентильном уровнях. При этом итерации могут касаться как модернизации только аппаратной и программных частей разрабатываемой системы, так и выбора того, какие из функций лучше реализовать программно, а какие – аппаратно.
Таким образом, система проектирования должна содержать средства, позволяющие при переходе от одного уровня к другому проверять, что поведение соответствует желаемому и при этом система удовлетворяет требованиям по быстродействию, обюему, потреблению. В следующем разделе рассматриваются вопросы проверки соответствия первому из указанных аспектов – «правильному поведению», которое в свою очередь подразделяется на функциональное (функциональная корректность) и временное (согласованность времен формирования результатов, что, очевидно, частично определяет также и быстродействие системы) и рассматривается в рамках «логической» верификации.
Проблема верификации
Итак, верификация проекта должна выполняться относительно соответствующей спецификации. Говоря о верификации, мы всегда предполагаем наличие некоторого «начального» – быть может, менее формального – описания системы.
Например, при синтезе RTL-модели устройства из сети FSM-машин, построенной из исходной спецификации системы, следует убедиться в правильности поведения полученной схемы, по крайней мере, быть уверенным, что все выходные векторы RTL- и FSM-моделей и их векторы состояний совпадают (естественно, с учетом способа кодирования состояний).
При переходе с алгоритмического уровня к некоторой аппаратной модели (скажем, RTL) один из возможных вопросов – это вопрос эквивалентности полученной в результате синтеза RTL-модели арифметической части устройства алгоритму вычисления. Так, при проектировании Фурье-процессоров следует удостовериться, что выбранная схемная реализация корректна, т.е. позволяет правильно (например, с требуемой точностью), вычислять спектральные последовательности.
Один из очевидных путей верификации состоит в моделировании (simulation, что наиболее точно отражается русскоязычным термином «имитационное моделирование») разрабатываемой системы на соответствующем уровне представления. Выполнив на некотором множестве инструкций и данных моделирование проекта на соответствующем уровне абстракции, можно было бы сравнить полученные результаты (например, значения всех бит выходных и внутренних линий в RTL) с результатами ожидаемыми (скажем, с результатами выполнения инструкций на уровне их двоичного представления). Сравнение должно быть организовано так, чтобы любые несоответствия результатов формировали флаг ошибки. Входные воздействия (поток команд и данных), на которых выполняется моделирование, могут генерироваться как псевдослучайная последовательность, где вероятности значений отдельных бит управляются весовыми коэффициентами, отражающими свойства инструкций. Существенно, что они должны инициировать работу различных блоков устройства и при этом быть чувствительными к всевозможным ошибкам реализации модели.
Очевидными функциональными ошибками являются ошибки в арифметических устройствах, приводящие к неправильным результатам выполнения операций (например, ошибки переноса в сумматоре). Должны формироваться соответствующие флаги при выполнении инструкций с неразрешенными операндами, ошибки выборки инструкций и данных в очередях конвейеризированных систем, при ошибках адресации памяти и т.д. Иными словами, при функциональной верификации стараются «спровоцировать» появление различных некорректных событий.
В качестве примера проектной ошибки, приводящей к временным задержкам, можно указать конфликты в конвейерных системах [17, 18].
Однако возникает естественный вопрос, позволяют ли наборы команд и данных, на которых выполняют моделирование проектируемой системы, обеспечить проверку правильности работы относительно некоторой спецификации. Иными словами – является ли проверка достаточно полной? Действительно, что с содержательной точки зрения означает утверждение, что арифметическое устройство с n входами, реализующее булеву функцию f(x1,...,xn), разработано правильно? Это означает, прежде всего, что на всех возможных 2n входных наборах на выходах спроектированной схемы должны формироваться результаты, равные f(x1,...,xn) на соответствующих наборах. Нетрудно представить, что значит промоделировать схему 64-разрядной вычислительной системы! Но ситуация оказывается существенно более драматичной, если схема с n входами имеет m ячеек памяти. В этом случае необходимо убедиться в правильности прохождения схемы через все возможные 2m состояний на 2n входных наборах (в действительности, значительное число состояний являются нерабочими или запрещенными). В практике разработки тестов для производственного контроля цифровых устройств размерность задачи перебора существенно снижают, опираясь на хорошо проверенное предположение, что неполадки в реальной схеме сводятся к так называемым «одиночным константным неисправностям» (под ними понимают «залипание» узла схемы в логический нуль или единицу), «коротким замыканиям» между проводниками, а также к специфической группе неисправностей, проявляющихся в КМОП-структурах. Поэтому входные наборы для проверки строят не из соображений проверки правильности работы схемы на всем множестве входных наборов, а из соображений активизации путей для каждой из неисправностей, в результате чего число входных наборов, на которых следует верифицировать возможность тестирования схемы, оказывается по большей части приемлемым для моделирования.
Мерой того, насколько исчерпывающим образом может проверить полученное множество входных векторов данное устройство, служит «полнота контроля», определяемая как отношение числа всех возможных в данном устройстве неисправностей из рассматриваемого класса, к числу неисправностей, проверяемых на полученном множестве тестовых векторов. При этом моделирование на псевдослучайных и «ручных», или функциональных, тестах (а иногда и автоматический синтез тестов) позволяют получать списки непроверенных неисправностей. Такие средства предусмотрены в составе всех основных САПР разработки цифровых систем, в том числе, в пакете TetraMAX компании Synopsis, FastGen от Mentor Graphic, IBM TestBench и т.д.
Чтобы верифицировать проекты устройств посредством моделирования их работы на разумно большом (но не полном!) множестве наборов команд и данных, было бы заманчиво иметь аналогичную характеристику для оценки полноты проверки относительно ошибок проектирования, которые приводят к тому, что разработанное устройство формирует неправильный результат хотя бы на одном из допустимых наборов команд и данных.
Для этого нужны модель ошибок и способ определения неправильного (ошибочного) поведения схемы. Очевидно, эта информация должна задаваться в терминах модели, используемой на рассматриваемом уровне проектирования.
Так, на уровне FSM-модели возможны следующие ошибки: дополнительное или отсутствующее состояние; неправильно заданные выходы; переход не в то состояние, которое должно быть в правильно функционирующей системе.
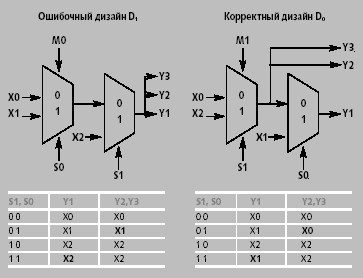
При синтезе RTL-модели из FSM-модели могут возникнуть следующие проектные ошибки [12]:
- ELF (extra latch/flip-flop): лишние триггеры в результате неправильного учета числа состояний FSM0;
- MSE (module substitution error): неверное замещение одного модуля модели (регистр, триггер, мультиплексор) другим, имеющим то же число входов и выходов, вследствие чего структура RTL-сети не нарушается;
- BOE (bus order error): некорректное упорядочивание бит в шине;
- BSE (bus source error): соединение входа некоторого модуля не с тем источником сигнала.
Наличие модели множества неисправностей позволяет помимо псевдослучайной генерации команд и данных («входных наборов») писать так называемые целевые тесты для проверки конкретных неисправностей (часто их также называют «ручными», в отличие от генерируемых псевдослучайных). При этом оба класса тестов (псевдослучайные и ручные) комбинируются, выполняясь последовательно один за другим.
Если за эталонное поведение проектируемой системы принимаются результаты выполнения инструкций (instruction set processing – ISP), то проверка RTL-модели может свестись к моделированию на входных наборах, выполнение которых может оказаться неверным из-за наличия аппаратных ошибок. Соответственно, по их совокупности и должна выполняться оценка полноты, чтобы оценить, можно ли из положительного результата прохождения обеих групп тестов (результаты моделирования RTL-модели совпадают с ISP) сделать вывод об отсутствии ошибок.
В настоящее время разработаны разнообразные средства для анализа полноты основанной на моделировании верификации проектов цифровых систем. Разумеется, главный вопрос – насколько используемая мера полноты соответствует возможным классам ошибок.
Меры полноты предложены для всех используемых уровней описания. Например, для FSM-модели можно использовать характеристику state-transition coverage, показывающую долю возможных переходов, которые активизируются рассматриваемым тестовым множеством [13]. Обычно эту характеристику применяют для оценки полноты верификации управляющих схем при использовании методологии проектирования, в которой в проектируемом устройстве отдельно описывают управляющую (control path) и, условно говоря, «арифметическую» части (data path). Оценка получается пессимистической, поскольку многие вызывающие эквивалентное поведение тесты будут рассматриваться как неэквивалентные.
Поскольку моделирование на соответствующем уровне проектирования является необходимым элементом разработки, вполне естественно желание оценить полноту верификации по наблюдениям трасс модели при моделировании на соответствующем (чаще всего, RTL) уровне. Трассы обычно представляются в терминах выполняемых команд, в них могут выделяться различные события, связанные с их (команд) выполнением, например, выполнение условных переходов. При этом сами переходы от одних событий к другим можно представить графом переходов некоторой FSM.
Так поступают, например, в системе оценки полноты CADET, используемой при разработке микропроцессоров Alpha [14]. Система строит диаграммы состояний, представляющих различные функции, реализуемые микропроцессором, и позволяет отобразить графически все существенные состояния и переходы узлами и дугами на графах состояний. Соответственно можно определить, какие из необходимых функций проверяются при моделировании («прогоне») RTL-модели процессора на конкретном множестве тестов, пополнив их, если полнота, по мнению разработчиков, недостаточна.
Очевидно, однако при использовании неформальных способов задания множества ошибок проектирования полнота оценки зависит от того, насколько мы «угадали» с моделями этих ошибок. При этом обюем моделирования может быть недопустимо велик по стоимости и затратам времени, занимая несколько суток при прогоне на современных высокопроизводительных рабочих станциях [4].
Для проектных ошибок, приводящих не к функциональным, а к временным некорректностям (особенно, если система реализована с теми или иными элементами параллелизма), рассмотренные методики оценки полноты через моделирование мало что дают. Например, чтобы смоделировать при псевдослучайном тестировании конфликты при обращении к данным по некоторому адресу, необходимо, чтобы входные случайные наборы сформировали подобную ситуацию. Малая вероятность подобных комбинаций предполагает наличие длинных входных последовательностей (сотни миллионов событий), что и приводит к уже упомянутым временным затратам. Еще большая проблема возникает при моделировании влияния на время выполнения конфликтов в конвейерных процессорах.
Поэтому давняя мечта разработчиков – получить в распоряжение автоматические (или по крайней мере достаточно автоматизированные) методы доказательства функциональной и временной корректности проектируемой системы. В современной практике эти мечты пытаются реализовать в рамках так называемых «формальных методов верификации».
Название это достаточно прозрачно: чтобы автоматизировать некоторый интеллектуальный процесс, его следует сначала формализовать. Однако в данном случае «формализация» имеет несколько иной смысл, чем это обычно понимают в математическом моделировании. Как правило, под формализацией какого-то описания системы понимается построение математической модели, позволяющей получать численные (или символические, но однозначно интерпретируемые) характеристики протекающих в системе процессов. Однако принятие решения о качестве системы в этом случае выполняется в результате содержательной интерпретации результатов, т.е. сам по себе вывод суждения о системе оказывается неформальным. Например, если мы, используя какую-либо математическую модель кэш-памяти, получим прогнозируемое значение промаха (скажем, 0,01), то решение о приемлемости этого значения должно быть принято конструктором системы, исходя из некоторого понимания о допустимой величине промаха при заданных требованиях к проектируемой системе.
Говоря же о формальной верификации проектов цифровых систем, подразумевают возможность получения однозначного ответа о корректности системы, имея лишь некоторое формальное описание результатов проектирования и исходной спецификации. При этом, под «формальностью» понимается то, что между символами («словами»), которые описывают (представляют) спецификацию, не существует никаких связей, кроме тех, которые явно описаны по тем или иным формальным правилам.
Итак, формальная верификация – это способ построения системы логического вывода об определенных свойствах некоторого описания, записанного в соответствии с определенными формальными правилами. Чтобы ее выполнить, необходимы [15, 16].
- Некоторое множество правил построения логических описаний ("формул") функционирования системы и набор семантических правил, задающих смысл каждой из формул.
- Множество правил построения логических описаний свойств системы, которые должны проверяться в процессе верификации, и семантические правила, которые задают, что означает, что данное свойство удовлетворяет системе.
- Правила вывода и алгоритмы проверки указанных "отношений сатисфакции".
Иными словами, в основе всех алгоритмов формальной верификации лежат те или иные алгоритмы анализа логических условий, в терминах которых описаны условия корректности.
В зависимости от принятых правил построения логических описаний и правил вывода, различают «логики», или «логические системы», в рамках которых можно делать выводы о соответствии или нет исходной спецификации.
Наверняка читатели имеют представление о логической системе, задаваемой так называемой «булевой алгеброй» с двумя операциями (например, отрицание и логическое И; остальные логические операции можно выразить через эти две), описывающей операции над двоичными данными, выполняемыми логическими элементами цифровых систем. Однако этой простейшей логической системы недостаточно для представления условий функционирования сложных систем. Прежде всего, условия корректности работы обычно трудно описать только с использованием элементарных булевых операций; нужен еще по крайней мере условный оператор if. Кроме того, сравнивать приходится спецификации разных уровней описания, например RTL с FSM, где кодировка состояний выполняется с использованием тех или иных «перечислимых» типов. Да и в RTL-моделях широко применяют операции как со словами, так и с отдельными битами. Поэтому в верификации цифровых систем предпочтительно применение так называемых расширенных пропозициональных логик. (Несколько упрощая, можно сказать, что для записи условий корректности проекта приемлемой оказывается не логика высказываний, а логика предикатов [15]).
|
| Рис. 2. Ошибка типа BSE в RTL-модели |
В первую очередь специфику логических выражений в формальной верификации определяют тем, какого рода свойства системы предполагается верифицировать – функциональные или временные. Иными словами, проверяем ли мы, что проектируемая система выполняет все свои функции функционально корректно (т.е. формирует ожидаемый результат) или же выполняет их корректно и «своевременно» (т.е. событие, состоящее в формировании на некотором узле схемы результата, в некотором смысле «правильно» позиционировано относительно других событий в проектируемой системе).
В функциональной верификации разрабатываемую систему рассматривают как некоторую функцию входов и выходов. Например, пусть ошибка состоит в том, что в схеме, которая должна реализовать булеву функцию y = G(x1,...,xn), из-за ошибки в RTL-модели одна из линий соединена с ошибочным входом (рис. 3). Логическое условие того, что ошибка будет обнаружена, состоит в том, что G(z, x2,...,xn)Б? G(x1,...,xn) всегда, когда z инверсно x1.
Если воспользоваться концепцией состояния системы и рассматривать проектируемую системы в терминах состояний-переходов (а сами состояния вычислять, скажем, по полученной RTL-модели), то условия корректного поведения схемы можно представить в терминах корректности переходов. Как правило, под состоянием понимают набор (вектор) двоичных значений входов, регистров и выходов схемы на RTL-уровне (для асинхронных схем может потребоваться более сложная конструкция). Работа схемы (ее поведение) описывается как переход из текущего состояния в следующее, под влиянием входного сигнала.
Приписав булеву переменную каждому узлу схемы, состояние схемы можно описать присвоением каждому узлу значения 0 или 1. Затем мы можем написать общее булево выражение, истинность которого определяется каждым конкретным присваиванием булевых значений в узлах схемы. Поведение схемы можно представить упорядоченным набором пар текущего и следующего состояний (V, V'), где V – переменные текущих состояний, а V' – переменные следующих состояний, в которые система переходит под воздействием соответствующего набора.
Пусть, например, V={v0, v1, v2} – набор переменных текущего состояния, а V'={v0', v1', v2'} – следующего, и они связаны между собой следующим образом:
v0' =vб?0
v1' = v0 » v1 (1)
v2' = (v0^v1) » v2
(Напомним, что б? – логическое отрицание, » – сложение по модулю 2, ^ – конююнкция).
Пусть R i(V,V'), i=1,2,...n – система логических выражений (1) на каждом из переходов. Тогда, если имеется представление устройства на уровне FSM, то верификация RTL-модели будет состоять в сравнении описания FSM (которая, напомним, является исходным описанием на синтез RTL-модели) с выражениями R(V,V') = R0(V,V') ^ ... ^ Rn-1(V,V'), представляющее описание результатов всех переходов, вычисленных по RTL-модели. Нетрудно видеть, что в этом случае верификация состоит в решении логических уравнений.
В качестве примера задания временных условий, покажем, как можно представить влияние ресурсных конфликтов на временное поведение некой программы, реализуемой на некотором процессоре с конвейером. [18].
Будем использовать следующие обозначения: r – рассматриваемый ресурс; Ii – инструкция в конвейере на фазе конвейеризации si, на цикле pj; t0i, t0j – моменты времени, в которые инструкции Ii, Ij выбираются в конвейер. Покажем, как можно определиить предикат ресурсного конфликта. Обозначим: r – рассматриваемый ресурс, Ii – инструкция в конвейере на фазе конвейеризации si, на цикле pj, t0i, t0j – моменты времени, в которые инструкции Ii Ij выбираются в конвейер. Тогда предикат ресурсного конфликта Resource_Conflict((Ii,t0i),(Ij,t0j),r) можно определить через извлекаемый из спецификации инструкций предикат Phase_used(Ip,sp,pj,r) как:
Resource_Conflict((Ii,t0i),(Ij,t0j),r):=si, sj,: pipeline_stage.
$ pj, pj: clock_phase.
(0<(t0j- t0i)) &((t0j+sj) = (t0j+sj)) &
(Phase_used(Ip,sp,pj,r)&Phase_used(Ij,sp,pj,r).
Здесь, как это принято в математической логике, символ $ означает квантор существования.
Подставляя конкретные значения переменных, можно определить истинность или ложность значения предиката и выяснить, выполняются ли условия отсутствия конфликта.
В настоящее время существуют различные языки спецификаций и трансляторы, позволяющие получать указанные логические уравнения из соответствующих спецификаций, которые стараются строить на базе тех или иных временных логик [19], позволяющих описывать порядок наступления событий (в том числе, и совместно протекающих).
Рассмотрим в качестве примера широко используемую в современных программных системах верификации временную логику [22]. Выражения временной логики состоят из так называемых временных соотношений выражений и «кванторов пути». Квантор всеобщности A соответствует высказыванию «для всех путей, образованных переходами из состояния в состояние», квантор существования E – высказыванию «для некоторых путей». Используются четыре вида временных соотношений.
- G ("всегда"). Выражение Gp означает, что логическое условия p выполняется в любой рассматриваемый момент времени.
- F ("в конце концов"). Fp означает, что в один из моментов времени событие p обязательно наступит.
- X ("в следующий момент времени"). Xp означает, что событие p наступит в следующий относительно текущего момент времени.
- U ("до тех пор, пока"). pUq означает, что p истинно до тех пор, пока не наступит q.
С помощью формул временной логики выражают условия (свойства) верифицируемой системы.
С точки зрения реализации методов верификации главный вопрос – о вычислительной сложности метода. Решение логических уравнений относится к классу переборных задач (комбинаторных), решение которых в общем случае требует выполнения огромного числа операций, число которых экспоненциально растет с числом переменных. Учитывая, что описание как функциональных, так и временных свойств RTL и вентильных моделей содержит сотни тысяч переменных, кажется, что применение формальных методов обречено. Однако некоторые современные математические «изобретения» в области комбинаторных методов (например, [23]) позволяют частично преодолеть эти трудности и применить формальную верификацию в практике разработки современных систем.
Мы не будем давать здесь изложение этих методов: чтобы дать сколько-нибудь ясное представление о них потребуется слишком много журнального места. (Хорошее описание основных математических методов, используемых в формальной верификации можно найти на http://www.afm.sbu.ac.uk/.)
Заключение
Основная мотивация деятельности по верификации проектов вычислительных систем состоит в «дороговизне» пропущенных ошибок. Идеальным решением была бы полностью формальная верификация. На первый взгляд, она вполне возможна. Ее реализация при использовании перечисленных программных средств не требует глубоких математических знаний; полезным может оказаться лишь общее понимание используемых математических моделей. Да и используемые языки представления спецификаций используют интуитивно понятную для разработчика аппаратуры нотацию.
К сожалению, алгоритмы формальной верификации подвержены явлению «комбинаторного взрыва» (связанное с экспоненциальным ростом пространства состояний системы), и время решения на «типичных» рабочих станциях оказывается недопустимо большим. Даже алгоритмы, являющиеся линейными по числу состояний, для логических функций с большим числом переменных оказываются неприменимыми.
В настоящее время удается верифицировать системы, описываемые уравнениями с несколькими сотнями переменных, тогда как верификационные модели современных микропроцессорных систем (причем после определенной декомпозиции на субмодели) содержат сотни тысяч переменных.
Поэтому процесс верификации требует комбинации формальных и неформальных методов моделирования на определенных входных наборах. В таблице 2 представлены результаты использования различных методов верификации. В рассмотренном в ней примере формальная верификация обеспечила обнаружение 24% ошибок; при этом только 36% найденных при формальной верификации ошибок можно было бы обнаружить при моделировании.
Примером продуманного сочетания различных средств верификации является инструментарий Cadence Integrated Solutions, обеспечивающий интеграцию системы формальной верификации FormalCheck с системами моделирования высокого уровня Cadence Virtual Component Co-design, функционального моделирования NC-Sim и высокоуровневого моделирования мультимедийных и коммуникационных систем на Signal Processing Worksystem.
В последнее время широко обсуждается еще одна важная практическая проблема формальной верификации. Это проблема полноты спецификации: действительно ли формальная спецификация проектируемой системы отражает все функционально-временные аспекты поведения системы [20, 21].
По сути, верификация проектов сложных цифровых систем на высоких уровнях спецификации превратилась в самостоятельный вид деятельности в процессе проектирования. Intel, IBM, Bell Labs и другие крупные производители имеют структурные подразделения верификации (причем специализированные по видам верификации – отделы моделирования, отделы формальной верификации, доказательства теорем и т.п.). Сокращение затрат на этом этапе проектирования является одной из наиболее актуальных задач, чтобы затраты на верификацию не превысили выгоды от своевременного выхода на рынок.
Литература
[1] W. Rosenstiel, Rapid Prototyping, Emulation and Hardware/Software Co-debugging. In System-Level Synthesis, ed. by A.A. Jerraya and J. Mermet, NATO Science Series, Kluwer Academic Publisher, 1998
[2] M. Blum, H. Wasserman, Reflections on the Pentium Division Bug. IEEE Trans. on Computers, vol. 45, no. 1996, 4, April
[3] Alpha 21264 Microprocessor Programer's Reference Manual. Compaq Computer, 2000
[4] Per Bjesse, Tim Leonard, Abdel Mokkedem, Finding Bugs in an Alpha Microprocessor Using Satisfability Solvers. in Proc. of 13th International Conference, CAV 2001, Paris, France, July 18-22, 2001, LNCS 2102
[5] Miroslav Velev, Randal Bryant, Bit-Level Abstraction in the Verification of Pipelined Microprocessors by Correspondence Checking. In Formal Methods in Computer-Aided Design, vol. 1522 of LNCS
[6] Стешенко, Примеры проектирования цифровых устройств с использованием языков описания аппаратуры. «Схемотехника», 2001, б№ 7
[7] S. Devadas, A.R. Newton, Decomposition and factorization of sequential finite state machines. IEEE Trans. on Computer-Aided Design, vol. 1989, 8, Nov.
[8] В.Е. Котов, Л.А. Черкасова, Исчисление процессов, в кн. «Системная информатика». Вып. 2, Новосибирск, «Наука», 1993
[9] M.K. Molloy, Performance Analysis Using Stochastic Petri Nets, IEEE Trans. on Computers, vol. C-31, 1982, September
[10] Hillston. Compositional Approach to Performance Modelling. Cambridge University Press, 1996
[11] Moataz Kamel, Stefan Leue, Formalization and validation of the General Inter-ORB Protocol (GIOP) using PROMELA and SPIN, International Journal on Software Tools for Technology Transfer, Abstract Volume 2, Issue 4, 2000
[12] David Van Campenhout, Hussain Al-Asaad, John P. Hayes, Trevor Mudge & Richard B. Brown, High-Level Design Verification of Microprocessors via Error Modeling. ACM Transactions on Design Automation of Electronic Systems, vol. 3, no. 4, 1997
[13] S. Palnitkar et al, Finite state machine trace analysis program, Proc. Int. Verilog HDL Conf., 1994
[14] Mike Kantrowitz, Lisa Noack, Functional Verification of a Multiple-issue, Pipelined, Superscalar Alpha Processor – the Alpha 21164 CPU Chip. Digital Technical Journal, vol. 7, no. 1, 1995
[15] О.П. Кузнецов, Г.М. Адельсон-Вельский, Дискретная математика для инженеров. М.: Энергоиздат, 1988
[16] Л.М. Лихтарников, Первое знакомство с математической логикой. СПб.: Лань, 1997
[17] В.А. Сигнаевский, Я.А. Коган, Методы оценки быстродействия вычислительных систем. М.: Наука, 1990
[18] F. Tahar, Formal Verif. in RISC processors EURO-DAC 1994, pp. 284-289.
[19] Amir Pnueli, Specification and development of reactive systems, Information Processing, vol. 86, 1986
[20] Yatin Hoskote, Timothy Kam, Pei-Hsin Ho, Xudong Zhao, Coverage Estimation for Symbolic Model Checking. DAC'99
[21] Hana Chockler et al, A Practical Approach to Coverage in Model Checking. In Proceedings of 13th International Conference, CAV 2001, Paris, France, July 18-22, 2001, LNCS 2102
[22] E. Clarke, O. Grumberg, D. Long, Model Checking, in Springer-Verlag Nato ASI Series F, Volume 152, 1996
[23] R. Bryant, Graph-based Algorithms for Boolean Function Manipulation. IEEE Trans. on Computers, vol. C-35, 1986, Aug.
