При решении конкретных задач иногда приходится сталкиваться с ограничениями универсальных инструментов, преодоление которых может осуществляться за счет разработки хитроумных методов. Однако это загромождает программу несущественными деталями. Между тем, есть инструменты, определяющие новый стиль программирования. Например, путем эволюционного наращивания мультиметодов можно создать процедурно-параметрическую парадигму.
Технологии, используемые в программировании, подвержены постоянным изменениям, но только самые крупные подвижки протекают на поверхности и затрагивают целые направления развития отрасли, поддерживаются огромными капиталовложениями и рекламной шумихой. Иногда для эффективного решения частных задач существующих средств оказывается недостаточно, что заставляет искать и новые методы, и инструменты. Авторы удачных находок заявляют миру о своей, пусть маленькой, но в чем-то привлекательной находке.
Для меня побуждающим мотивом явился поиск путей эволюционного расширения мультиметодов [1]. Пытаясь преодолеть вложенную проверку типов в процедурном подходе, я пришел к давно открытой двойной диспетчеризации. Она поразила своей неуклюжестью и стимулировала поиск более приемлемых решений, нашедших отражение в статье, где акцент был сделан больше на внешнее оформление расширяемых мультиметодов, чем на их реальную внутреннюю поддержку [2]. В конце концов, был сделан вывод о несовместимости объектно-ориентированного программирования и эволюции мультиметодов; поиск сконцентрировался на процедурных решениях.
Ряд трюков, описанных в [1], найдены недавно и совершенно случайно. Они показывают, что объектный подход может поддерживать эволюционную разработку. Однако рассмотренные приемы ведут к появлению жесткой связи между добавляемыми классами и к увеличению размера интерфейсов у потомков. Сохраняется также основной недостаток объектного подхода, определяемый привязкой методов к данным: появление новых методов (и мультиметодов) изменяет всю иерархию уже созданных классов. Как и в образцах проектирования [3], попытка безболезненного развития одного параметра ведет к жесткой привязке другого.
Даже прямая процедурная реализация в целом выглядит более естественной. Вызов мультиметода по форме и содержанию эквивалентен вызову любой другой процедуры. Использование RTTI позволяет непосредственно проверять типы родственных объектов и обеспечивает вызов специализированных обработчиков. Иерархия классов при этом включает только методы, нацеленные на обработку внутренних данных. Отсутствуют вспомогательные процедуры, осуществляющие дополнительное связывание. Говорить же об эволюции программы в этом случае не приходится.
Путь к методу
В своем окончательном решении Скотт Мейерс тоже воспользовался внешними процедурами [4], однако его версия программы опирается на моделирование таблицы виртуальных методов. Предложим альтернативное решение, обеспечивающее непосредственную индексацию функций, отвечающих за реализацию альтернативных составляющих. Чтобы не перегружать читателя кодом, остановлюсь лишь на констатации общих принципов. Полную программную реализацию можно найти в [5].
Основная специфика эволюционного расширения при процедурном подходе проявляется через независимость данных от функций, их обрабатывающих. Это позволяет отказаться от метафоры эволюционной пирамиды, заменив ее волнообразным расширением методов, связанным с добавлением новых типов данных.
В принципе, подобное расширение можно осуществлять с использованием обычных структур; мы сохраним классы для более гибкой реализации обычных виртуальных методов (например, функции вывода).
Реализация волнообразного наращивания может опираться на непосредственное построение матрицы отношений между взаимодействующими классами. В случаях прямой и реверсивной двойной диспетчеризации [2] проблему индексации можно решить, применив специальную переменную класса, задающую его ранг в иерархии. Использование мультиметодов в качестве внешних процедур позволяет упростить организацию базового класса, определяющего лишь общие параметры чисел:
class Number {
public:
// Вывод значения числа в стандартный поток
virtual void StdOut() = 0;
// Конструктор, обеспечивающий установку ранга
Number(int r): _rank(r) {}
// Получить ранг класса
int GetRank() { return _rank;}
private:
// Число, задающее ранг класса
int _rank;
};Конструирование производных классов осуществляется независимо друг от друга и по одинаковой схеме. Порядок их следования в иерархии не влияет на внутреннюю структуру, но затрагивает реализацию конструкторов и подключение процедур, осуществляющих обработку отдельных альтернатив. Начнем эволюцию, например, с целочисленных данных. Соответствующий класс будет выглядеть так:
// Класс целых чисел, первый в эволюции классов
class Int: public Number {
public:
void StdOut() {cout<<"It is Int.
Value="<Внутренняя организация методов вполне традиционна, необходимо только зафиксировать конкретный ранг класса в его конструкторе в соответствии с порядком следования в эволюционной иерархии:
// Ранг класса
const int intRank = 0;
// Конструктор, обеспечивающий инициализацию
числа
Int::Int(int v): Number(intRank), _value(v) {}
Далее можно реализовать обработчик вычитания для уже существующих комбинаций. Пока это вычитание целого числа из целого:
// Обычное вычитание одного целого числа
из другого
Int* SubIntInt(Int& n1, Int& n2) {
return new Int(n1._value - n2._value);
}
Для использования написанной функции в мультиметоде необходимо обобщить аргументы:
// Обобщающее вычитание одного целого числа
из другого
Number* SubIntInt(Number& n1, Number& n2) {
Int* pInt1;
Int* pInt2;
// Динамическая проверка типа
// для исключения ошибок программиста
if( (pInt1 = dynamic_cast(&n1)) &&
(pInt2 = dynamic_cast(&n2)) ) {
// Оба типа соответствуют условиям проверки
return SubIntInt(*pInt1, *pInt2);
}
else {
// Ошибка в типах; возможно формирование
исключения
return 0;
}
}
Аналогичные манипуляции сопровождают добавление нового класса, например, действительного числа:
class Double: public Number {
public:
void StdOut() {cout<<"It is Double.
Value="<Реализация методов должна учитывать установку в конструкторе нового ранга:
// Ранг класса
const int doubleRank = 1;
// Конструктор, обеспечивающий
// инициализацию числа
Double::Double(double v): Number(doubleRank),
_value(v) {}
Функции вычитания добавляются, обеспечивая реализацию нового «фронта нарастающей волны»; по своей организации они практически не отличаются от целочисленного вычитания.
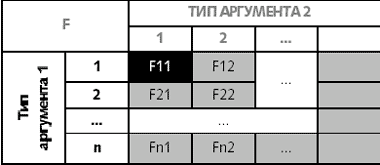
Наличие у классов ранга, присутствие специализированных функций и их обобщенного интерфейса позволяют выстроить матрицу, задающую параметрические отношения между отдельными функциями вычитания и их операндами-специализациями. В качестве индексов, обеспечивающих выбор нужных функций, используются ранги экземпляров классов. Матрица содержит указатели на функции вычитания с одинаковыми сигнатурами:
Number* SubXXX(Number& n1, Number& n2);
Достаточно информации только о прототипах:
// Функция, полученная при добавлении
// к программе первого класса
Number* SubIntInt(Number& n1, Number& n2);
// Функции, полученные при добавлении
// к программе второго класса
Number* SubIntDouble(Number& n1, Number& n2);
Number* SubDoubleInt(Number& n1, Number& n2);
Number* SubDoubleDouble(Number& n1, Number& n2);
// Количество классов
int const numbers = 2;
// Общее описание типа обобщающих функций
typedef Number* (*SubFunPtr)(Number& n1,
Number& n2);
// Матрица мультиметодов
static SubFunPtr subtMatr[numbers][numbers] =
{
// Добавлено при создании первого класса
SubIntInt,
// Добавлено при создании второго класса
SubIntDouble, SubDoubleInt, SubDoubleDouble
};
Окончательное сокрытие реализации обеспечивается дополнительной функцией, определяющей интерфейс с клиентом:
// Функция вычитания, использующая
// множественный полиморфизм
Number* operator- (Number& n1, Number& n2)
{
SubFunPtr fun = subtMatr[n1.GetRank()]
[n2.GetRank()];
if(fun) // Проверка на присутствие функции
return fun(n1, n2);
else
return 0; // или генерация исключения
}
Преодоление проблемы «общих знаний»
Лобовое решение допускает раздельное написание отдельных классов, но не спасает от сведения разрозненных знаний в одно место. Это происходит при окончательном формировании матрицы отношений между операндами и ведет к нарушению эволюционного развития кода. В идеале хотелось получить вариант, который обеспечил бы независимое добавление и мультиметодов, и классов, поддерживая, тем самым, не только безболезненное расширение, но и повторное использование.
Добавление мультиметодов при процедурном подходе осуществляется без модификации кода, так как функции находятся вне данных. «Развязать» добавление классов можно, если обеспечить их независимость от значения ранга. Это можно сделать за счет автоматического ранжирования во время запуска программы. Используем класс Number для подсчета числа производных классов и максимального ранга:
class Number {
public:
virtual void StdOut() = 0;
// Получение ранга
virtual int GetRank() = 0;
protected:
static int _max_rank; // Максимальный ранг
системы классов
};
Виртуальная функция GetRank() выдает значение ранга и переопределяется в наследниках. Ранг может храниться в статической переменной конкретного производного класса, обеспечивая тем самым общий ключ для всех его экземпляров. Производные классы не зависят друг от друга, разрабатываются и включаются в проект в любом порядке. Для большей их независимости следует использовать различные единицы компиляции. Класс целых чисел выглядит так:
// Класс целых чисел; теперь может быть любым
в эволюции
class Int: public Number {
public:
void StdOut();
int GetRank();
// Конструктор, обеспечивающий инициализацию
числа
Int(int v);
public:
// Значение целого числа
int _value;
private:
static int _rank; // Ранг всех целых чисел
};
Аналогично создаются и другие добавляемые классы, а их методы размещаются в отдельных единицах компиляции. Кроме этого, необходимо инициализировать ранг начальным значением, сигнализирующим об отсутствии регистрации (используется отрицательное число). Регистрацию классов надо провести до выполнения основной программы; в примере она осуществляется созданием регистрационного экземпляра. Независимость от порядка инициализации и уникальность экземпляра обеспечивается использованием образца Singleton, реализованного по Мейерсу [6] в виде статической переменной функции. Для целочисленных величин рассматриваемое решение выглядит следующим образом:
// Ранг целочисленного класса
int Int::_rank = -1;
// Вывод значения числа в стандартный поток
void Int::StdOut() {
cout << "It is Int. Value = " << _value
<< endl;
}
// Получение ранга класса
int Int::GetRank() {return _rank;}
// Конструктор
Int::Int(int v): _value(v) {
if(_rank == -1) _rank = _max_rank++;
}
// Функция, реализующая образец Singleton,
// обеспечивающий единственность
регистрационного
// экземпляра и его автоматическое
// создание при первом обращении
Int& GetRegInt() {
static Int regInt(0);
return regInt;
}
«Гвоздем» программы является класс Matrix, задающий массив указателей на функции, которые осуществляют альтернативные вычитания. Он поддерживает вставку обработчиков специализаций, автоматическое изменение размерности при добавлении новых специализаций, получение указателя на функцию по рангам ее аргументов. Внутри вместо матрицы используется одномерный массив.
// Тип обобщающих функций
typedef Number* (*FunPtr)(Number& n1,
Number& n2);
class Matrix {
public:
// Вставка в матрицу очередного метода
// на место, указанное индексами
void Insert(FunPtr fun, int i, int j);
// Получение специализированной функции
по ее индексам
FunPtr GetFun(int i, int j);
private:
// создание "матрицы" большей размерности
и перенос
// в нее ранее накопленных данных
void Replace(int new_size);
public:
// Конструктор класса
Matrix(): _fun_matr(0), _size(0) {}
// Деструктор, осуществляющий очистку
// массива указателей на функции
~Matrix() {if(_fun_matr) delete[] _fun_matr;}
private:
// Массив указателей на специализированные
// мультиметоды вычитания cоздается
динамически
// (вместо матрицы)
FunPtr* _fun_matr;
// Текущий размер матрицы
int _size;
};
Метод вычитания взаимодействует с экземпляром матрицы, заполненной указателями на специализации. Как и при регистрации классов, для формирования матрицы до момента ее использования, применяется образец Singleton в виде статической переменной функции.
// Вместо матрицы используется функция,
// обращающаяся к статически заданной матрице.
// Реализуется образец Singleton,
// обеспечивающий единственность экземпляра и
// автоматическое создание при первом обращении.
Matrix& GetSubtMatr() {
static Matrix subtMatr;
return subtMatr; }
// Функция вычитания, использующая
// множественный полиморфизм
Number* operator- (Number& n1, Number& n2) {
Matrix& subtMatr = GetSubtMatr();
FunPtr tmp_fun = subtMatr.GetFun(n1.GetRank(),
n2.GetRank());
if(tmp_fun) // Проверка на присутствие
указателя
return tmp_fun(n1, n2);
else
return 0; // или генерация исключения
}
Заполнение матрицы происходит автоматически, по мере подключения к проекту новых специализаций; независимость регистрации обеспечивает гибкость. Ранг обработчика во многом определяется последовательностью сборки проекта. Единица компиляции, описывающая вычитание одного целого числа из другого, может выглядеть так:
#include "IntClass.h"
#include "Matrix.h"
// Доступ к регистрационному классу для целых
чисел
Int& GetRegInt();
// Доступ к матрице мультиметодов
Matrix& GetSubtMatr();
// Специализированное (обычное) вычитание
одного целого числа из другого
Int* SubIntInt(Int& n1, Int& n2) {
return new Int(n1._value - n2._value);
}
// Обобщающее вычитание одного целого
числа из другого.
// Аргументы являются ссылками на базовый
// класс, что обеспечивает их общую
параметризацию
Number* SubIntInt(Number& n1, Number& n2) {
Int* pInt1; Int* pInt2;
// Динамическая проверка типа для исключения
// ошибок программиста
if( (pInt1 = dynamic_cast(&n1)) &&
(pInt2 = dynamic_cast(&n2)) ) {
// Оба типа соответствуют условиям
return SubIntInt(*pInt1, *pInt2);
} else { // Ошибка в типах. Возможно
// формирование исключения
return 0;
}
}
// Регистрация функции, определяющей
// отношение вычитания между двумя
целочисленными классами
namespace { // Описание соответствующего
класса
class regIntInt {
public:
// Конструктор, отвечающий за регистрацию
regIntInt() {
Int& regInt = GetRegInt();
// В соответствии с рангом класса
// осуществляется занесение регистрируемой
// функции в вектор указателей на
специализации
int Int_rank = regInt.GetRank();
Matrix& subtMatr = GetSubtMatr();
subtMatr.Insert(SubIntInt, Int_rank,
Int_rank);
}
};
// Использование регистрирующего
класса
regIntInt IntIntFun;
} // namespace
Аналогичным образом реализуется вычитание для других вариантов специализаций.
Монометод
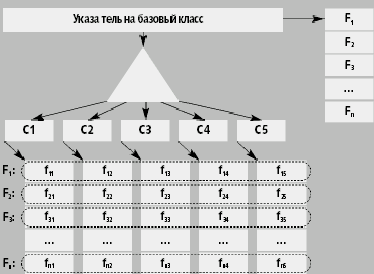
Когда число аргументов мультиметода уменьшается до одного, множественный полиморфизм становится эквивалентен объектно-ориентированному, а мультиметод вырождается в «монометод». Их различие лишь в том, что полиморфный метод Fi при объектном подходе просто «размывается» по множеству таблиц виртуальных функций производных классов C1-Ck, поддерживающих отдельные специализации F1i-Fki. Пример, демонстрирующий реализацию объектного полиморфизма для пяти производных классов, приведен на рис. 1.
|
| Рис. 1. Реализация полиморфизма через таблицы виртуальных функций при использовании объектного подхода |
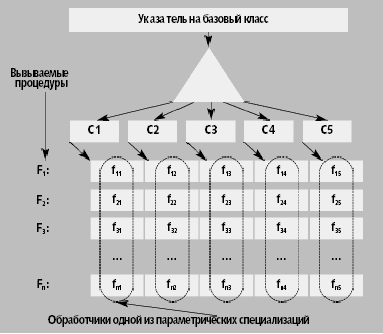
Процедурная версия монометода может опираться на размещение всех специализаций в одномерном массиве. Вызов альтернативы осуществляется в зависимости от ранга аргумента. В этом случае специализации Fi не прикрепляются к таблицам виртуальных функций отдельных классов, а располагаются независимо, что обеспечивает большую гибкость. Иллюстрирующий этот подход рис. 2 показывает, что объектно-ориентированный полиморфизм ортогонален процедурному по техническому исполнению.
|
| Рис. 2. Организация альтернатив при параметрическом полиморфизме |
Построение монометода можно рассмотреть на примере функции вывода. Указатели на отдельные специализации хранятся в классе Vect. Использование класса vector из стандартной библиотеки шаблонов позволяет упростить реализацию.
// Задание типа обобщающих функций вывода
typedef void (*MonoFunPtr)(Number& n1);
class Vect {
public:
// Вставка в вектор очередного метода на место,
// указанное индексом
void Insert(MonoFunPtr fun, int i);
// Получение специализированной функции по ее
индексу
MonoFunPtr GetFun(int i);
private: // Для реализации вектора
используется STL
vector _fun_vec;
};
// Вставка в матрицу очередного метода на место,
// указанное индексами
void Vect::Insert(MonoFunPtr fun, int i){
if(i < _fun_vec.size()) _fun_vec[i] = fun;
else { // Расширяем до указанного i размера
с обнулением
_fun_vec.insert(_fun_vec.end(),
i - _fun_vec.size() + 1, 0);
_fun_vec[i] = fun;
}
}
// Получение специализированной функции
по ее индексам
MonoFunPtr Vect::GetFun(int i)
{ return _fun_vec[i]; }
Обобщенный вывод опирается на единичный экземпляр вектора (Singleton), параметризирующего соответствующие специализации. Функция обобщенного вывода Out выбирает специализацию по рангу выводимого класса. Ее действия полностью дублируют метод класса StdOut.
// Вектор, параметризирующий функции вывода
Vect& GetOutVect() {
static Vect outVect; return outVect;
}
// Функция вывода, использующая
// параметрический полиморфизм.
void Out(Number& n1) {
Vect& outVect = GetOutVect();
MonoFunPtr tmp_fun = outVect.GetFun
(n1.GetRank());
if(tmp_fun) // Проверка на присутствие
указателя
tmp_fun(n1);
else
; // или генерация исключения
}
Разработка специализаций и их регистрация осуществляются так же, как и при создании функции вычитания. Пример показывает, что существует техническая реализация, ортогональная использованию виртуальных методов классов, которая является частным случаем множественного полиморфизма.
Навстречу новой парадигме
Рассмотренные примеры демонстрируют принципы построения повторно используемых и эволюционирующих мультиметодов. Существует множество трюков, расширяющих возможности представленного кода и обеспечивающих его эффективное применение в реальных приложениях. Можно даже построить библиотеку, скрывающую специфику внутренней организации. Хотелось бы затронуть несколько иную тему — разработку инструментальных средств, напрямую поддерживающих множественный полиморфизм.
Есть разные пути развития систем программирования в этом направлении, зачастую взаимно дополняющие друг друга. Можно, например, сформулировать общие требования, разработать методологические концепции, а затем попытаться воплотить их в соответствующих технологиях и инструментах. Примером могут служить методы безболезненного развития программ [7], опирающиеся на выделение горизонтальных и вертикальных слоев. Альтернативным направлением является попытка облечь базовые понятия, данные и процедуры, в конструктивные оболочки, обеспечивающие необходимые эффекты за счет создания инструментов, над которыми затем выстраиваются парадигмы и методологические концепции. В этом направлении особенно преуспел объектно-ориентированный подход, подаваемый сегодня в качестве средства для решения чуть ли не всех проблем.
Методы, представленные в статье, предлагают технические решения, которые, двигаясь снизу, достаточно просто воплотить в соответствующие конструктивы. В этом случае большая часть работы, связанной с регистрацией данных и процедур, ляжет на транслятор, а окончательное формирование параметрических отношений может проводиться во время статической или динамической компоновки, в крайнем случае, во время инициализации данных. В распоряжение программиста можно предоставить язык, поддерживающий множественный полиморфизм, который по своим возможностям перекрывает полиморфизм объектно-ориентированный.
В рамках этого подхода предложена процедурно-параметрическая парадигма программирования [8-10], основная особенность которой — опора на уже существующий процедурный подход. Этот механизм доступен через набор абстракций, синтаксис и семантика которых обеспечивают более гибкое добавление новых обработчиков специализаций и альтернативных типов данных без изменения уже написанного кода.
Создание объектно-ориентированных языков программирования привело к инструментальной поддержке их трех основных китов: наследованию, инкапсуляции и полиморфизму. Отпала необходимость писать процедурный код, моделирующий соответствующие эффекты, что упростило создание расширяемых программ и повторно используемых модулей. Однако многие проблемы эволюционного программирования остались нерешенными, в том числе и разработка мультиметодов.
Развитие систем и методов программирования показывает, что процедурные языки тоже могут успешно манипулировать указанными понятиями. В Обероне Вирт успешно использовал механизм наследования для построения абстрактных типов данных. Мейерс [11] показал, что внешние функции улучшают инкапсуляцию. Предлагаемое в статье процедурно-параметрическое расширение языков позволяет реализовать альтернативные методы, перекрывающие по своим возможностям объектный подход. В целом же можно сказать, что не существует особых причин безоговорочно верить в то, что эволюционная разработка и повторное использование кода могут эффективно поддерживаться лишь объектно-ориентированной парадигмой.
Литература
[1] Легалов А. ООП, мультиметоды и пирамидальная эволюция. — «Открытые системы», 2002, №3
[2] Легалов А.И. Разработка программ на основе объектно-реляционной методологии. — Математическое обеспечение и архитектура ЭВМ: Сб. научных работ. Вып. 2. КГТУ, Красноярск, 1997
[3] Гамма Э., Хелм Р., Джонсон Р., Влиссидес Дж. Приемы объектно-ориентированного проектирования. Паттерны проектирования. Пер. с англ. — СПб.: Питер, 2001
[4] Мейерс С. Наиболее эффективное использование C++. 35 новых рекомендаций по улучшению ваших программ и проектов: Пер. с англ. — М.: ДМК Пресс, 2000
[5] Легалов А.И. Эволюция мультиметодов при процедурном подходе. — http://www.softcraft.ru/coding/evp/evp.shtml, 2002
[6] Мейерс С. Эффективное использование C++. 50 рекомендаций по улучшению ваших программ и проектов. Пер. с англ. — М.: ДМК, 2000
[7] Горбунов-Посадов М.М. Расширяемые программы. — М.: Полиптих, 1999
[8] Легалов А.И. Процедурно-параметрическая парадигма программирования. Возможна ли альтернатива объектно-ориентированному стилю? — Деп. рук. № 622-В00 Деп. в ВИНИТИ 2000.13.03
[9] Легалов А.И. Процедурно-параметрическое программирование. — http://www.softcraft.ru/paradigm/ppp/ppp01.shtml, 2001
[10] Легалов А.И., Швец Д.А. Процедурно-параметрические расширения языка программирования Оберон-2. — Вестник Красноярского государственного технического университета. Вып. 23. Математические методы и моделирование. Красноярск, 2001
[11] S. Meyers. How Non-Member Functions Improve Encapsulation. C/C++ User Journal, February, 2000
Александр Легалов (lai@softcraft.ru) — сотрудник Красноярского государственного технического университета.
