Авторы статьи описывают алгоритмы, затрагивающие решение трех классических задач добычи данных: анализ рыночной корзины (market basket analysis), кластеризация (clustering) и классификация (classification).
Крупные компании в течение десятков лет накапливали данные о своих клиентах, поставщиках, продуктах и услугах. Благодаря высоким темпам развития электронной коммерции работающие в Web начинающие фирмы могут превратиться в огромные предприятия буквально в течение нескольких месяцев, а не то что лет. И, как следствие, будут стремительно расти и их базы данных. Технология добычи данных (data mining), которую иначе называют обнаружением знаний в базах данных (knowledge discovery in databases [1]), предоставляет организациям инструментарий, позволяющий анализировать большие собрания информации в поисках тенденций, шаблонов и взаимосвязей, способных помочь в принятии стратегических решений.
Традиционно сложилось так, что в алгоритмах анализа данных предполагается, что входные базы данных содержат относительно небольшое число записей. Однако размер современных баз данных слишком велик, в силу чего их невозможно полностью разместить в основной памяти. Извлечение данных с жесткого диска происходит заметно медленнее доступа к данным, находящимся в оперативной памяти. Поэтому, для того чтобы методы добычи данных, используемые для работы с очень большими базами данных, стали эффективными, они должны обладать значительным уровнем масштабируемости. Алгоритм называют масштабируемым (scalable), если при неизменной емкости основной памяти с увеличением числа записей во входной базе данных время его работы растет линейно.
В последнее время исследователи сосредоточили свои усилия на изучении масштабируемых алгоритмов добычи данных в сверхбольших наборах данных. В данном обзоре будет описан достаточно широкий диапазон алгоритмов, решающих три классические задачи добычи данных.
Анализ рыночной корзины
Рыночная корзина - это набор товаров, приобретенных покупателем в рамках одной отдельной транзакции, что является весьма характерной операцией - к примеру, ею описываются и результаты визита в бакалейную лавку или интерактивная покупка в виртуальном магазине, таком как Amazon.com. Регистрируя все бизнес-операции в течение всего времени своей деятельности, торговые компании накапливают огромные собрания таких транзакций. Одна из самых распространенных задач, решаемых при проведении анализа подобных баз данных, состоит в поиске товаров или наборов товаров (itemset), которые одновременно встречаются во многих транзакциях. Каждый из шаблонов поведения покупателей, выявленных благодаря такому анализу, описывается перечнем входящих в набор товаров и числа транзакций, содержащих эти наборы. Торговые компании могут использовать эти шаблоны для того, чтобы более правильно разместить товары в магазинах или изменить структуру страниц товарных каталогов и страниц Web.
Набор, состоящий из i товаров, называется i-элементным набором (i-itemset). Процент транзакций, содержащих данный набор, называется обеспечением (support) набора. Принято считать, что для того чтобы набор представлял интерес, его обеспечение должно быть выше определенного пользователем минимума; такие наборы называют часто встречающимися (frequent).
В таблице 1 приведено описание трех транзакций, хранящихся в реляционной базе данных. В соответствующей таблице пять полей: идентификатор транзакции, идентификатор пользователя, приобретенный им товар, цена и дата транзакции. Первая транзакция показывает, что покупатель приобрел компьютер, MS Office и Doom. В данном примере, 2-элементный набор {жесткий диск, Doom} имеет обеспечение в 67%.
| TID | CID | Товар | Цена | Дата |
| 101 | 201 | Компьютер | 1500 | 1/4/99 |
| 101 | 201 | MS Office | 300 | 1/4/99 |
| 101 | 201 | Doom | 100 | 1/4/99 |
| 102 | 201 | Жесткий диск | 500 | 1/7/99 |
| 102 | 201 | Doom | 100 | 1/7/99 |
| 103 | 202 | Компьютер | 1500 | 1/24/99 |
| 103 | 202 | Жесткий диск | 500 | 1/24/99 |
| 103 | 202 | Doom | 100 | 1/24/99 |
Почему поиск часто встречающихся наборов представляет собой нетривиальную задачу? Во-первых, число транзакций может оказаться чрезвычайно велико и обычно данные обо всех из них «не помещаются» в памяти. Во-вторых, потенциальное число часто встречающихся наборов растет экспоненциально с ростом количества товаров в наборе, хотя реальное число часто встречающихся наборов может оказаться намного меньше. В примере, приведенном на рисунке 1, упоминаются четыре различных продукта, поэтому существует 2^4 - 1 = 15 потенциально часто встречающихся наборов.
 |
| Рис. 1. Пример иерархии типа is-a |
Алгоритм Apriori
Данный алгоритм определяет часто встречающиеся наборы за несколько этапов. На i-ом этапе определяются все часто встречающиеся i-элементные наборы. Каждый этап состоит из двух шагов: формирование кандидатов (candidate generation) и подсчет кандидатов (candidate counting). Рассмотрим i-ый этап. На шаге формирования кандидатов алгоритм создает множество кандидатов из i-элементных наборов, чье обеспечение пока не вычисляется. На шаге подсчета кандидатов алгоритм сканирует базу данных транзакций, вычисляя обеспечение наборов-кандидатов. После сканирования алгоритм отбрасывает кандидатов, обеспечение которых меньше определенного пользователем минимума и сохраняет только часто встречающиеся i-элементные наборы.
Во время 1-го этапа выбранное множество наборов-кандидатов содержит все 1-элементные наборы. Алгоритм вычисляет их обеспечение во время шага подсчета кандидатов. Таким образом, после первого этапа известны все часто встречающиеся 1-элементные наборы. Что представляют собой наборы-кандидаты, выбранные во время шага выбора кандидатов второго этапа? Рассуждая прямолинейно, в кандидаты можно «записать» все пары товаров. Однако Apriori сокращает множество наборов-кандидатов отсеивая - априори - тех кандидатов, которые не могут быть часто встречающимися, основываясь на полученной на предыдущих этапах информации о том, какие из наборов являются часто встречающимися. Отсев происходит на основе простого предположения о том, что если набор является часто встречающимся, все его подмножества также должны быть часто встречающимися. Таким образом, перед началом шага подсчета кандидатов алгоритм может отвергнуть любой набор-кандидат, подмножество которого не является часто встречающимся.
Рассмотрим базу данных, представленную в таблице 1. Предположим, что минимальное принимаемое в расчет обеспечение равно 60%, поэтому набор будет часто встречающимся, если он присутствует по крайней мере в двух транзакциях. На первом этапе все товары по отдельности являются наборами-кандидатами и подсчитываются во время шага подсчета кандидата. На втором этапе кандидатом может стать только пара товаров, каждый из которых является часто встречающимся. Например, набор {MS Office, Doom} не является кандидатом, поскольку на первом этапе было определено, что подмножество {MS Office} не является часто встречающимся. Таким образом, на втором этапе алгоритм сформирует следующий список наборов-кандидатов: {компьютер, Doom}, {жесткий диск, Doom} и {компьютер, жесткий диск}. На третьем этапе после подобного отсева не останется ни одного набора-кандидата. Набор {компьютер, жесткий диск, Doom} будет априори отсеян, поскольку его подмножество {компьютер, жесткий диск} не является часто встречающимся. Таким образом, с учетом того, что минимальное обеспечение равно 60%, в приведенной в качестве примера базе данных часто встречающиеся наборы и значения их обеспечений таковы:
- {компьютер} 67%,
- {жесткий диск} 67%,
- {Doom} 100%,
- {компьютер, Doom} 67%,
- {жесткий диск, Doom} 67%.
Apriori подсчитывает не только обеспечение всех часто встречающихся наборов, но также и обеспечение тех наборов-кандидатов, которые не могли быть отброшены априори. Множество всех наборов-кандидатов, которые встречаются редко, но чье обеспечение алгоритм Apriori вычисляет, называется негативной областью (negative border). Таким образом, набор принадлежит к негативной области, если его нельзя отнести к часто встречающимся, но все его подмножества таковыми являются. В нашем примере негативная область состоит из наборов {MS Office} и {компьютер, жесткий диск}. Все подмножества наборов в негативной области являются часто встречающимися; в противном случае этот набор был бы удален еще на шаге априорного отсеивания.
Оптимизация алгоритма Apriori
Apriori сканирует базу данных несколько раз, в зависимости от размера самого длинного часто встречающегося набора. Было предложено несколько усовершенствований этого алгоритма, которые позволяют сократить число сканирований базы данных, число наборов-кандидатов при каждом сканировании, или и то, и другое.
Разбиение. Эшок Савасере и его коллеги [3] разработали алгоритм, который требует всего два сканирования базы данных с транзакциями. База данных разбивается на непересекающиеся разделы, каждый из которых достаточно мал, чтобы разместиться в оперативной памяти. На первом шаге алгоритм читает каждый раздел и в каждом из них с помощью Apriori определяет «локально» часто встречающиеся наборы.
При втором сканировании алгоритм подсчитывает обеспечение всех локально часто встречающихся наборов относительно всей базы данных. Если набор является часто встречающимся относительно всей базы данных, он должен быть часто встречающимся по крайней мере в одном разделе; следовательно, при втором сканировании определяется супермножество всех потенциально часто встречающихся наборов.
Хеширование. Джонг Су Парк и его коллеги [4] предложили использовать вероятностный подсчет для сокращения числа наборов-кандидатов, подсчитываемых на каждом этапе выполнения алгоритма Apriori. Такое сокращение обеспечивается за счет того, что каждый из k-элементных наборов-кандидатов помимо шага сокращения проходит шаг хеширования.
Во время выбора кандидата на этапе k-1 алгоритм создает хеш-таблицу. Каждая запись в хеш-таблице - это счетчик, в котором накапливается сумма всех обеспечений k-элементных наборов, которые соответствуют этой конкретной записи в хеш-таблице. Алгоритм использует эту информацию на этапе k для сокращения множества k-элементных наборов-кандидатов. После сокращения подмножества, как это происходит в Apriori, алгоритм может удалить набор-кандидат, если его значение в хеш-таблице меньше порогового значения, установленного для обеспечения.
«Выборочный» анализ. Ханну Тойвонен [5] предложил алгоритм, который, как правило, требует всего два сканирования базы данных. Данный алгоритм сначала извлекает произвольный экземпляр из базы данных и формирует множество наборов-кандидатов, которые с высокой вероятностью в полной базе данных будут часто встречающимися. При последующем сканировании базы данных алгоритм подсчитывает точные значения обеспечения для этих наборов и обеспечение их негативной области. Если ни один из наборов в негативной области не является часто встречающимся, то алгоритм уже выявил все часто встречающиеся наборы. В противном случае, некоторое супермножество наборов в негативной области может быть часто встречающимися, но их обеспечение еще не вычислено. Алгоритм выборки определяет и подсчитывает все такие потенциально часто встречающиеся наборы при последующем сканировании базы данных.
Динамический подсчет наборов. Сергей Брин и его коллеги [6] предложили алгоритм Dynamic Itemset Counting (DIC), который разбивает базу данных на несколько блоков, отмеченных так называемыми «начальными точками» (start point), и циклически сканирует базу данных. В отличие от Apriori, DIC может добавлять новые наборы-кандидаты в любой начальной точке, а не только в начале нового сплошного сканирования базы данных. В каждой начальной точке DIC оценивает обеспечение всех наборов, которые уже выбраны, и добавляет новые наборы к множеству наборов-кандидатов, если все его подмножества оцениваются как часто встречающиеся.
Если DIC добавляет все часто встречающиеся наборы и их негативную область к множеству кандидатов во время первого сканирования, то во время второго сканирования в некоторой точке он получит точные значения обеспечения каждого набора и, таким образом, работа DIC будет завершена за два сканирования.
Расширения и обобщения
Несколько исследователей предложили рассмотреть расширения классической задачи поиска часто встречающихся наборов.
Иерархия is-a. Одно из таких расширений предполагает рассмотрение иерархии is-a товаров из базы данных. Иерархия is-a определяет, какие из товаров являются конкретизацией, а какие обобщением других товаров. Например, как показано на рисунке 1, товары {компьютер, жесткий диск} можно объединить в товарную группу «аппаратное обеспечение». Расширенная задача состоит в анализе типичных наборов, в состав которых входят товары различных уровней иерархии.
Наличие иерархии изменяет представление о том, когда товар присутствует в транзакции. В дополнение к товарам, перечисленным непосредственно, анализируются и их товарные группы. Это позволяет определить связи, входящие в более высокие уровни иерархии, поскольку обеспечение набора может увеличиваться, если вместе с товаром подсчитывается и вхождение его товарной группы.
Рассмотрим пример иерархии, приведенный на рисунке 1. Кроме набора {компьютер, MS Office} следует также анализировать наборы, включающие такие «наборы», как «аппаратное обеспечение» и «программное обеспечение». В базе данных из таблицы 1 обеспечение набора {компьютер, MSOffice} равно 33%, в то время как обеспечение набора {компьютер, программное обеспечение} равно 67%.
Один из подходов к определению часто встречающихся наборов при наличии иерархии состоит в том, чтобы умозрительно расширить каждую транзакцию за счет использования прототипов всех товаров в транзакциях. Любой алгоритм для определения часто встречающихся наборов может теперь применяться в расширенной базе данных. Оптимизация этой примитивной стратегии описана Ракешем Агравалом и Рамакришнаном Срикантом [7].
Типичные последовательности покупок. Каждому покупателю можно сопоставить последовательность его транзакций, упорядоченных по времени. Это делает оправданной постановку следующей задачи: выявить последовательности наборов, которые многие покупатели приобрели примерно в том же порядке [7, 8]. Для каждого покупателя входная база данных состоит из упорядоченной последовательности транзакций. Для заданной последовательности наборов процент последовательностей транзакций, которые ее содержат, называется обеспечением последовательности наборов.
Последовательность транзакций содержит последовательность наборов, если каждый набор содержится в одной транзакции и верно следующее: если i-ый набор в последовательности наборов содержится в j-ой транзакции в последовательности транзакций, (i+1)-ый набор в последовательности наборов содержится в транзакции с номером, большим, чем j. Цель поиска последовательных шаблонов состоит в том, чтобы найти все последовательности наборов, которые имеют обеспечение выше, чем определенный пользователем минимум. Последовательность наборов является часто встречающейся, если ее обеспечение превышает этот минимум.
В таблице 1, покупателю 101 сопоставлена последовательность [{компьютер, MS Office}, {жесткий диск, Doom}]. Эта последовательность транзакций содержит последовательность наборов [{MS Office}, {жесткий диск}].
Календарный анализ рыночной корзины (Calendric market basket analysis). Сридхар Рамасвами и его коллеги [9] используют временную метку, присваиваемую каждой транзакции, для формулировки задачи календарного анализа рыночной корзины. При том, что обеспечение набора может не быть большим по отношению ко всей базе данных, оно может быть больше на ее подмножестве, которое удовлетворяет определенным временным ограничениям.
С другой стороны, в определенных случаях, наборы, которые являются часто встречающимися во всей базе данных, могут «накопить» свое обеспечение только на определенных подмножествах. Одна из задач календарного анализа рыночной корзины состоит в том, чтобы найти определенные временные интервалы, в рамках которых оказываются часто встречающимися все наборы, определенные пользователем.
Кластеризация
Кластеризация предполагает распределение объектов по нескольким группам таким образом, что в общую группу попадают похожие объекты. Обратимся вновь к базе данных из таблицы 1. Предположим, что для того, чтобы объединить покупателей в кластер с учетом их предпочтений при покупках, мы для каждого покупателя вычисляем общее количество и среднюю стоимость всех купленных ими товаров. В таблице 2 представлена информация о девяти покупателях, распределенных по трем кластерам. Покупатели, отнесенные к первому кластеру, купили мало дорогих товаров, покупатели во втором кластере купили много дорогих товаров, а покупатели в третьем кластере приобрели мало дешевых товаров. (Данные в таблице 2 не соответствуют таблице 1, поскольку ранее мы рассматривали лишь несколько транзакций.)
| Иденти-фикатор | Зарплата | Воз-раст | Работа | Груп-па |
| 1 | 30 тыс. | 30 | Предпринимательство | C |
| 2 | 40 тыс. | 35 | Промышленность | C |
| 3 | 70 тыс. | 50 | Наука | C |
| 4 | 60 тыс. | 45 | Предпринимательство | B |
| 5 | 70 тыс. | 30 | Наука | B |
| 6 | 60 тыс. | 35 | Промышленность | B |
| 7 | 60 тыс. | 35 | Предпринимательство | A |
| 8 | 70 тыс. | 30 | Предпринимательство | A |
| 9 | 40 тыс. | 45 | Промышленность | C |
Задача кластеризации рассматривается во многих областях, в том числе в статистике, машинном обучении и биологии. Однако ранее во всех этих приложениях масштабируемость алгоритма не выдвигалась во главу угла; исследователи всегда предполагали, что весь набор данных можно полностью поместить в оперативную память; главный упор всегда делался на улучшение качества кластеризации. Как следствие, эти алгоритмы нельзя применять для обработки сверхбольших наборов данных. В последнее время разработано несколько новых алгоритмов, в которых вопросам масштабирования уделяется большее внимание, в том числе к таким новым алгоритмам относятся обобщенное представление кластеров (summarized cluster representation), выборка и использование структур данных, поддерживаемых нижележащими СУБД.
Обобщенные представления кластеров
Тьян Занг и его коллеги [10] предложили алгоритм Birch, в котором благодаря обобщенным представлениям кластеров процедура кластеризации множества данных выполняется быстрее и при этом обладает большим масштабированием. В Birch реализована двухэтапная кластеризация. Сначала формируется предварительный набор кластеров, а затем к этому набору для выявления «истинных кластеров» применяются другие — пригодные для работы в оперативной памяти — алгоритмы кластеризации. Приведем следующую аналогию: если каждый элемент данных представить себе как бусину, лежащую на поверхности стола, то кластеры бусин можно «заменить» теннисными шариками и перейти к более детальному изучению кластеров теннисных шариков. Число бусин может оказаться достаточно велико, однако диаметр теннисных шариков можно подобрать таким образом, чтобы на втором этапе можно было, применив традиционные алгоритмы кластеризации, определить действительную сложную форму кластеров. Над масштабируемыми методами кластеризацией работают сейчас и другие исследователи, ставя перед собой задачу преодолеть присущие алгоритму Birch ограничения. При этом они в разных вариантах применяют идею обобщенного представления кластера.
Модель Birch*. В некотором смысле кластер соответствует области повышенной плотности объектов. В Birch эта идея нашла отражение в выделении обобщенного представления совокупности объектов, описываемое так называемой кластерной характеристикой (CF - cluster feature). Кластерная характеристика представляет собой тройку, состоящую из следующих компонентов: число точек в кластере, «центр тяжести» и радиус, где радиус кластера определяется как среднеквадратичное отклонение точек кластера от его центра тяжести. При добавлении новой точки в кластер новое значение CF можно вычислить на основе старого значения; нет необходимости учитывать параметры всех точек в кластере. Инкрементальный алгоритм Birch использует это свойство CF и поддерживает только характеристики кластеров, а не множества точек во время сканирования данных. Использование идеи кластерных характеристик оказывается эффективным по двум причинам.
- Они занимают намного меньше места, чем исходные представления, которые полностью описывают все объекты в кластере.
- Они удобны для вычисления всех внутрикластерных и межкластерных параметров, которые используются при принятии решений относительно кластеров. Более того, эти вычисления выполняются значительно быстрее, чем при использовании всех объектов в кластере. Например, расстояние между кластерами, радиусы кластеров, кластерные характеристики (и, следовательно, другие свойства) объединенных кластеров очень эффективно вычисляются по значениям CF для отдельных кластеров.
В алгоритме Birch для определения значений CF применяются векторные операции, такие как сложение, вычитание, вычисление центра тяжести и так далее. Таким образом, используемое в Birch определение кластерной характеристики не может быть экстраполировано на наборы, содержащие данные ряда типов, для которых эти операции не определены (например, символьные строки).
Концепции CF и CF-дерева, используемые в Birch, получили обобщение в модели Birch* [11], что позволило предложить два новых масштабируемых алгоритма кластеризации для данных в пространстве с произвольной метрикой. Эти новые алгоритмы позволят, к примеру, разделить множество {университет штата Висконсин в Мэдисоне, университет штата Висконсин в Уайт-Уотере, университет штата Техас в Остине, университет штата Техас в Арлингтоне} на два кластера университетов штатов Висконсин и Техас.
Другие работы, связанные с концепцией CF. Пол Бредли и его коллеги [12] использовали идеи CF для разработки целого класса масштабируемых интерактивных алгоритмов кластеризации, получившего название K-Means. Стартуя с некоторого первоначального разбиения множества данных, в этих итерационных алгоритмах кластеризации точки многократно переносятся из одного кластера в другой, пока не будет найдено распределение, соответствующее оптимальному значению некоторой критериальной функции.
Функционирование данной модели основано на выделении множеств сокращаемых (discardable) точек, сжимаемых (compressible) точек и точек основной памяти. Реальная точка является сокращаемой, если ее вхождение в кластер может быть восстановлено; алгоритм удаляет реальные точки и вместо всех них сохраняет только значением CF.
Точка является сжимаемой, если она не является сокращаемой, но принадлежит к так называемому компактному подкластеру (tight subcluster) - множеству точек, которые всегда делят членство в одном кластере. Такие точки могут перемещаться из одного кластера в другой, но при этом всегда перемещаются вместе. Такой подкластер подменяется своим значением CF.
Точка относится к точкам основной памяти, если она не является ни сокращаемой, ни сжимаемой. Как следует из названия, точки этого типа сохраняются в оперативной памяти. Итерационный алгоритм кластеризации перемещает только точки основной памяти и CF сжимаемых точек между кластерами до тех пор, пока не будет найдено оптимальное значение критериальной функции.
Гхоламхозейн Шейкхолеслами и его коллеги [13] предложили WaveCluster, алгоритм кластеризации на основе волновых преобразований. Сначала данные обобщаются путем наложения на пространство данных многомерной решетки. Вместо отдельных точек в дальнейшем анализируются обобщенные характеристики, суммирующие точки, которые попали в одну и ту же ячейку решетки. Такая обобщенная информация обычно умещается в оперативной памяти. Затем WaveCluster применяет волновое преобразование к обобщенным данным, чтобы определить кластеры.
Другие подходы
Среди других известных алгоритмов кластеризации для больших наборов данных мы хотели бы упомянуть еще три подхода. Реймонд Нг и Джавей Хан [14] предложили алгоритм Clarans, который формулирует задачу кластеризации как случайный поиск в графе. При использовании этого алгоритма совокупность узлов графа представляет разбиение множества данных на определенное пользователем число кластеров. Критериальная функция определяет «качество» кластера. Clarans сортирует пространство решений - все возможные разбиения множества данных - в поисках приемлемого решения. Случайный поиск решения останавливается в том узле, где достигается минимум среди предопределенного числа локальных минимумов. Судипто Гуха и его коллеги [15] предложили CURE - алгоритм иерархической кластеризации. В алгоритме DBScan Мартин Истер и его коллеги [16] понятие кластера формулируется с использованием концепции плотности (density).
Классификация
Предположим, что при помощи кластеризации накопленных данных о покупках, мы идентифицировали три различные группы покупателей, как показано в таблице 2. Предположим, что мы приобрели список рассылки с демографической информацией о потенциальных клиентах и хотели бы для каждого человека в списке рассылки определить, к какой из трех групп он относится, с тем, чтобы послать ему каталог, адаптированный в соответствии с пристрастиями этого конкретного человека.
В этой типичной для приложений добычи данных задаче уже накопленная информация о покупателях используется для того, чтобы предсказать вхождение в кластерах новых покупателей.
Наша база данных с накопленной информацией, также называемая иногда обучающей (training) базой данных, содержит записи с несколькими атрибутами. Один из атрибутов является зависимым (dependent), а другие - прогнозирующими (predictor) атрибутами. Цель состоит в том, чтобы построить модель, которая использует прогнозирующие атрибуты в качестве входных параметров и получает значение зависимого атрибута.
Если зависимый атрибут является численным, задача называется задачей регрессии (regression problem); в противном случае она называется задачей классификации (classification problem). Мы остановимся на задачах классификации, хотя аналогичные методики применимы и к задаче регрессии. Назовем значения зависимого атрибута метками классов (class label). В таблице 3 показан пример обучающей базы данных с тремя прогнозирующими атрибутами: зарплата, возраст и работа. Группа - это зависимый атрибут.
Исследователи предложили множество моделей классификации [17]: нейронные сети, генетические алгоритмы, методы байесовых сетей, логарифмически-линейные и другие статистические методы, таблицы решений и модели с древовидными структурами — так называемые классификационные деревья (classification tree). Классификационные деревья, также называемые деревьями решений (decision tree), представляют большой интерес в области добычи данных по нескольким причинам.
- Их интуитивное представление упрощает понимание классификационной модели.
- Конструирование деревьев решений не требует, чтобы аналитик определял какие-либо входные параметры.
- Точность прогноза деревьев решений равна или выше, чем у других классификационных моделей.
- Быстрые, масштабируемые алгоритмы могут быть использованы для построения деревьев решения на сверхбольших обучающих базах данных.
Каждый внутренний узел дерева решений помечается прогнозирующим атрибутом, называемым атрибутом расщепления (splitting attribute) и каждый узел-лист помечается меткой класса. Каждая ветвь, идущая от внутреннего узла, помечается предикатом расщепления, который затрагивает только атрибут расщепления данного узла. Предикаты расщепления характеризуются тем, что любая запись будет использовать уникальный путь от корня только к одному узлу-листу. Объединенная информация об атрибутах расщепления и предикатах расщепления в узле называется критерием расщепления (splitting criterion). На рисунке 2 изображено возможное дерево решения для обучающей базы данных из таблицы 3.
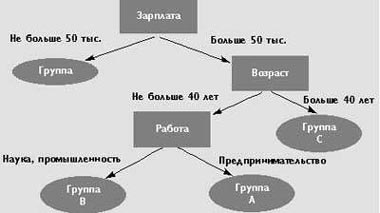 |
| Рис. 2. Пример дерева решений для каталожной рассылки |
Алгоритмы конструирования дерева решений состоят из двух этапов: создание дерева (tree building) и сокращение (pruning). При создании дерева выполняется следующая нисходящая процедура. Начиная с корневого узла алгоритм проверяет базу данных для определения локально «наилучшего» критерия расщепления. Затем он разбивает базу данных в соответствии с критерием расщепления и применяет процедуру рекурсивно. Затем дерево сокращается для того, чтобы его размер не вышел из под контроля. Некоторые алгоритмы построения дерева решений разделяют этапы создание дерева и сокращение, в то время как другие чередуют их для того, чтобы избежать необязательного наращивания некоторых узлов. На рисунке 3 приведен пример программы создания дерева.
 |
| Рис. 3. Пример программы для этапа создания дерева |
Выбор критерия расщепления определяет качество дерева решений и является объектом весьма напряженных исследований. Кроме того, если обучающая база данных не умещается в оперативной памяти, нам необходим масштабируемый метод доступа к данным. Один из таких методов - алгоритм Sprint, предложенный Джоном Шафером и его коллегами [18], предъявляет минимальные требования к необходимому объему памяти и представляет собой масштабируемый вариант популярного метода выбора расщепления CART. Другой подход - оболочка RainForest [19], предлагает широкий класс методов выбора расщепления, но в данном случае требования к памяти зависят от числа различных значений атрибутов во входной базе данных.
Sprint. Данный алгоритм построения классификационного дерева позволяет избежать зависимости между емкостью основной памяти и размером множества данных. Sprint создает классификационные деревья с помощью расщеплений надвое, требует отсортированного доступа к каждому атрибуту каждого узла. Для каждого атрибута алгоритм создает список атрибутов (attribute list), который представляет собой вертикальное разбиение обучающей базы данных D. Для каждого кортежа t, принадлежащего D, запись для t в списке атрибутов состоит из проекции t на атрибут, атрибута метки класса и идентификатора записи для t. Список атрибутов каждого атрибута создается в начале работы алгоритма и сортируется всякий раз в порядке возрастания значений атрибута.
В корневом узле алгоритм сканирует все списки атрибутов, пытаясь определить критерий расщепления. Затем он распределяет каждый список атрибутов между дочерними узлами корневого узла с помощью хеш-соединения со списком атрибутов расщепляемого атрибута. Идентификатор записи, который дублируется в каждом атрибуте, устанавливает связь между различными частями кортежа. Во время хеш-соединения алгоритм читает и распределяет каждый список атрибутов последовательно, что позволяет сохранить первоначальный порядок сортировки списка атрибутов. Затем алгоритм рекурсивно применяется к каждому из разбиений.
RainForest. Оболочка RainForest [19] действует исходя из предпосылки, что почти всем методам выбора расщепления нужна только обобщенная информация, чтобы определить критерий расщепления в узле. Эта обобщенная информация может быть получена в виде относительно компактной структуры данных, получившей название группа меток классов значений атрибутов (attribute-value class label group), или группа AVC.
Рассмотрим корневой узел в дереве. Пусть D - обучающая база данных. Множество AVC прогнозирующего атрибута A - это проекция D на A, где число индивидуальных меток классов является обобщенным параметром. Группа AVC в узле содержит наборы AVC всех прогнозирующих атрибутов. Рассмотрим базу данных, представленную на рисунке 4. Группа AVC корневого узла показана в таблице 4.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
Размер группы AVC узла пропорционален не числу записей в обучающей базе данных, а числу различных значений атрибута. Таким образом, в большинстве случаев группа AVC оказывается значительно меньше, чем обучающая база данных и обычно помещается в основной памяти. Учитывая, что группа AVC содержит всю информацию, которая нужна любому методу выбора расщепления, задача масштабирования существующего метода выбора расщепления теперь сводится к задаче эффективного конструирования группы AVC в каждом узле дерева.
Один достаточно простой метод доступа к данным основан на последовательном сканировании обучающей базы данных с целью создания группы AVC для корневого узла в основной памяти. Метод выбора расщепления затем вычисляет расщепление корневого узла. На следующем сканировании каждая запись считывается и добавляется к одному из дочерних разбиений. Затем алгоритм рекурсивно выполняется на каждом из дочерних разбиений.
Раджив Растожи и Кейсеок Шим [20] разработали алгоритм Public, который чередует создание дерева и его сокращение. Public стремится сократить узлы, которые при создании дерева не нужно наращивать дальше, тем самым экономя на затратах на конструировании некоторых узлов в дереве.
Большинство современных исследований, касающихся технологий добычи данных, предполагают, что данные статичны. На практике же данные содержатся в хранилищах, которые постоянно обновляются за счет добавления записей целыми пакетами. Принимая во внимание такое положение дел, можно быть уверенными, что будущие исследования должны быть направлены на разработку алгоритмов эффективного поддержания моделей и методов измерения изменений характеристик данных.
Современная парадигма добычи данных напоминает парадигму традиционных систем управления базами данных. Пользователь инициирует добычу данных и ждет получения результата. Но аналитиков интересуют оперативные, частичные и приблизительные результаты, которые можно уточнить с помощью нескольких последовательных запросов. Таким образом, исследования в будущем должны переориентироваться на то, чтобы сделать добычу данных более интерактивной.
Наконец, Web - самое большое хранилище структурированных, полуструктурированных и совсем не структурированных данных. Динамическая природа Сети, а также огромное разнообразие данных, которые она содержит, ставят грандиозные задачи перед исследователями.
Об авторах
Венкатеш Ганти (Venkatesh Ganti) - соискатель докторской степени в университете штата Висконсин (Mэдисон). Среди его основных научных интересов - анализ больших наборов данных и мониторинг изменений характеристик данных.
Йоханнес Герке (Johannes Gehrke) - соискатель докторской степени в университете штата Висконсин. Среди его основных научных интересов масштабируемые методы добычи данных, производительность алгоритмов добычи данных, а также добыча и мониторинг меняющихся наборов данных.
Раджу Рамакришнан (Raghu Ramakrishnan) - профессор факультета компьютерных наук университета штата Висконсин. Среди его основных научных интересов - языки баз данных, сетевые базы данных, добыча данных и интерактивная визуализация информации.
С Ганти, Герке и Рамакришнаном можно связаться по электронной почте по адресам {vganti, johannes,raghu}
Литература
[1] U.M. Fayyad et al., eds. Advances in Knowledge Discovery and Data Mining, AAAI/MIT Press, Menlo Park, Calif., 1996.
[2] R. Agrawal et al., «Fast Discovery of Association Rules», Advances in Knowledge Discovery and Data Mining, U.M. Fayyad et al., eds., AAAI/MIT Press, Menlo Park, Calif., 1996, pp. 307-328.
[3] A. Savasere, E. Omiecinski, and S. Navathe, «An Efficient Algorithm for Mining Association Rules in Large Databases», Proc. 21st Int?l Conf. Very Large Data Bases, Morgan Kaufmann, San Francisco, 1995, pp. 432-444.
[4] J.S. Park, M.-S. Chen, and S.Y. Philip, «An Effective HashBased Algorithm for Mining Association Rules», Proc. ACM SIGMOD Int?l Conf. Management of Data, ACM Press, New York, 1995, pp.175-186.
[5] H. Toivonen, «Sampling Large Databases for Association Rules», Proc. 22nd Int?l Conf. Very Large Data Bases, Morgan Kaufmann, San Francisco, 1996, pp. 134-145.
[6] S. Brin et al., «Dynamic Itemset Counting and Implication Rules for Market Basket Data», Proc. ACM SIGMOD Int?l Conf. Management of Data, ACM Press, New York, 1997, pp. 255-264.
[7] R. Agrawal and R. Srikant, «Mining Sequential Patterns», Proc. 11th Int?l Conf. Data Eng., IEEE CS Press, Los Alamitos, Calif., 1995, pp. 3-14.
[8] H. Mannila, H. Toivonen, and A.I. Verkamo, «Discovering Frequent Episodes in Sequences», Proc. 1st Int?l Conf. Knowledge Discovery Databases and Data Mining, AAAI Press, Menlo Park, Calif., 1995, pp. 210-215.
[9] S. Ramaswamy, S. Mahajan, and A. Silbershatz, «On the Discovery of Interesting Patterns in Association Rules», Proc. 24th Int?l Conf. Very Large Data Bases, Morgan Kaufmann, San Francisco, 1998, pp. 368-379.
[10] T. Zhang, R. Ramakrishnan, and M. Livny, «Birch: An Efficient Data Clustering Method for Large Databases», Proc. ACM SIGMOD Int?l Conf. Management of Data, ACM Press, New York, 1996, pp. 103-114.
[11] V. Ganti et al., «Clustering Large Datasets in Arbitrary Metric Spaces», Proc. 15th Int?l Conf. Data Eng., IEEE CS Press, Los Alamitos, Calif., 1999, pp. 502-511.
[12] P. Bradley, U. Fayyad, and C. Reina, «Scaling Clustering Algorithms to Large Databases», Proc. 4th Int?l Conf. Knowledge Discovery and Data Mining, AAAI Press, Menlo Park, Calif., 1998, pp. 9-15.
[13] G. Sheikholeslami, S. Chatterjee, and A. Zhang, «WaveCluster: A Multi-Resolution Clustering Approach for Very Large Spatial Databases», Proc. 24th Int?l Conf. Very Large Data Bases, Morgan Kaufmann, San Francisco, 1998, pp. 428-439.
[14] R.T. Ng and J. Han, «Efficient and Effective Clustering Methods for Spatial Data Mining», Proc. 20th Int?l Conf. Very Large Data Bases, Morgan Kaufmann, San Francisco, 1994, pp. 144-155.
[15] S. Guha, R. Rastogi, and K. Shim, «CURE: An Efficient Clustering Algorithm for Large Databases», Proc. ACM SIGMOD Int?l Conf. Management of Data, ACM Press, New York, 1998, pp. 73-84.
[16] M. Ester et al., «A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise», Proc. 2nd Int?l Conf. Knowledge Discovery Databases and Data Mining, AAAI Press, Menlo Park, Calif., 1996, pp. 226-231.
[17] D. Michie, D.J. Spiegelhalter, and C.C. Taylor, Machine Learning, Neural and Statistical Classification,» Ellis Horwood, Chichester, UK, 1994.
[18] J. Shafer, R. Agrawal, and M. Mehta. «SPRINT: A Scalable Parallel Classifier for Data Mining», Proc. 22nd Int?l Conf. Very Large Data Bases,» Morgan Kaufmann, San Francisco, 1996, pp. 544-555.
[19] J. Gehrke, R. Ramakrishnan, and V. Ganti, «RainForest- a Framework for Fast Decision Tree Construction of Large Datasets», Proc. 24th Int?l Conf. Very Large Data Bases, Morgan Kaufmann, San Francisco, 1998, pp. 416-427.
[20] R. Rastogi and K. Shim, «Public: A Decision Tree Classifier that Integrates Building and Pruning», Proc. 24th Int?l Conf. Very Large Data Bases, Morgan Kaufmann, San Francisco, 1998, pp. 404-415.
Venkatesh Ganti, Johannes Gehrke, Raghu Ramakrisnan. Mining Very Large Databases. IEEE Computer, August 1999, pp. 38-45. Raprinted with permission, Copyright IEEE, 1999, All rights reserved.
