Графический анализ данных в системе STATISTICA

Графики и диаграммы - один из самых наглядных способов представления результатов исследований. Загляните в любой научный или научно-популярный журнал - в большинстве статей основной результат показан на графике. Посетите конференцию, семинар или презентацию - и вы обязательно увидите плакаты или слайды с графическим изображением основных характеристик, схем или отчетных данных.

Практически каждый исследователь или аналитик на определенном этапе анализа данных непосредственно сталкивается с необходимостью представления полученных результатов в графическом виде: будь то отчет для руководителя, подготовка журнальной статьи или, наконец, просто процесс изучения. Графики являются неотъемлемой частью большинства процедур статистического анализа данных - факторного, кластерного, дисперсионного анализа, многомерного шкалирования, анализа соответствий или построения деревьев классификации.

Помимо специальных графических пакетов, предназначенных исключительно для подготовки рисунков и картинок, сегодня появляется все больше прикладных программ, содержащих удобный и достаточно мощный графический интерфейс, который позволяет превратить процедуру создания графических изображений в быстрый, логичный, необременительный, а зачастую и автоматизированный процесс.

Можно отметить некоторые общие тенденции развития отрасли программного обеспечения и направления совершенствования пакетов математической обработки данных. Эти программные продукты уже, как правило, нельзя назвать просто «программами», в большинстве своем они все больше трансформируются в некую интерактивную среду, которая сочетает в себе широкий набор алгоритмов, возможности программирования и графический интерфейс. Многие из них прошли долгий путь от первых версий с командной строкой до современного варианта с дружественным пользователю графическим интерфейсом.

Подобные тенденции можно наблюдать и среди программных пакетов для статистической обработки данных. К этому ПО сегодня предъявляются новые требования - им уже недостаточно поддерживать простой набор алгоритмов для реализации классических статистических методов. Совершенно необходима интеграция с другими программами, возможности импорта и экспорта данных, настраиваемый интерфейс и встроенный язык программирования для создания пользовательских алгоритмов.

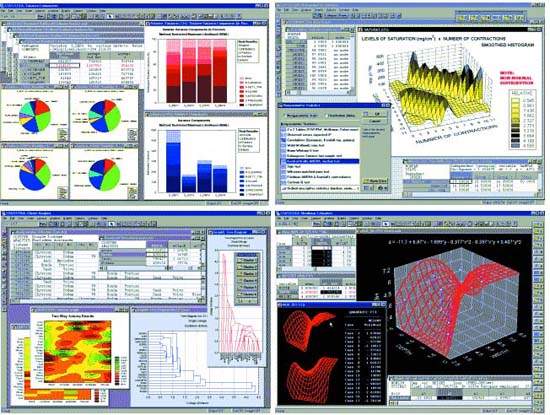Рис. 1. Пример окна с различными вариантами графиков

Сегодня, среди программных продуктов такого класса можно отметить систему STATISTICA, в которой реализовано более сотни вариантов различных типов графического представления данных (рис. 1). Все они доступны на любом этапе исследования и анализа результатов, а каждый полученный график можно отредактировать, связать с данными, сохранить, автоматически занести в отчет или вывести на печать. Профессиональная система STATISTICA для статистической обработки данных не только содержит все современные методы анализа, но и предлагает пользователю графический интерфейс, включающий сотни типов графического представления данных и широкий спектр методов настройки.

Необходимость графического представления результатов возникает на любом этапе обработки данных, начиная от разведочного графического анализа и заканчивая созданием итогового отчета о результатах исследований. Как правило, пользователю в первую очередь требуются традиционные двумерные и трехмерные гистограммы и диаграммы рассеяния, различные виды поверхностей и карт линий уровня, круговые диаграммы и диаграммы диапазонов. Однако существуют и более сложные типы графических представлений - матричные, тернарные и категоризованные графики, а также графики из пиктограмм для анализа многомерных данных. В данной статье акцент будет сделан на наиболее интересных и не совсем традиционных способах графического представления и анализа данных.

Матричные графики

Для исследования взаимосвязи между переменными файла данных можно для каждой пары переменных построить последовательность диаграмм рассеяния. В общем случае это достаточно длительный и трудоемкий процесс. Чтобы упростить эту процедуру, были придуманы так называемые матричные графики, которые представляют собой целые матрицы диаграмм рассеяния, линейных графиков или столбчатых диаграмм. Фактически такой график - это наглядное представление корреляционной матрицы. На рис. 2 показан пример диалогового окна для задания параметров и построенный матричный график для пяти переменных.

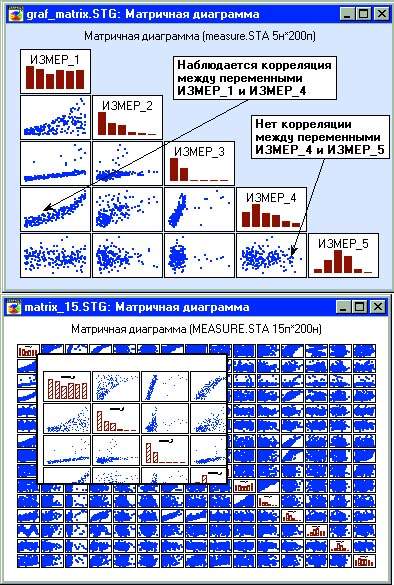Рис. 2. Матричные графики для различного числа переменных

Анализируя приведенные диаграммы, можно сделать первые выводы о взаимосвязи переменных, определить, какие из них коррелируют между собой, а какие нет. Построив матричный график для очень большого числа переменных, можно затем исследовать его с помощью процедуры увеличения изображения. Заметим, что возможности настройки графиков не ограничиваются только редактированием заголовков и изменением цветов и шаблонов. Можно поместить в графическое окно любые необходимые надписи, стрелки, различные фигуры. Кроме того, имеется возможность построения составных графиков с помощью технологии связывания и внедрения объектов (OLE). Например, на рис.2 увеличенный элемент помещен на исходный график в виде внедренного объекта и сохраняет все свои качества, в том числе и возможность независимого редактирования.

Итак, вместо того, чтобы анализировать попарные корреляции на отдельных диаграммах рассеяния (числом n(n-1)/2, где n число переменных), был построен один матричный график, с помощью которого можно найти группы переменных, наиболее тесно связанных друг с другом и которые следует проанализировать в первую очередь. Такой метод представляет собой один из вариантов так называемого разведочного анализа данных и дает возможность «охватить взглядом» исследуемую структуру.

Интерактивное закрашивание

Попробуем теперь более подробно рассмотреть и проанализировать зависимости между отдельными переменными, например, на диаграммах рассеяния. Как правило, любой график, построенный по данным исходной таблицы, остается связанным с этими данными (если такая функция специально не отменена пользователем). Подобный способ взаимодействия графиков и электронной таблицы используется во многих программах, поскольку позволяет автоматически отображать на графике все вносимые в таблицу изменения. Представим теперь, что имеется несколько графиков, но требуется изменить данные только для одного из них. Для этого существует специальное средство, называемое интерактивным закрашиванием. Это чрезвычайно удобный инструмент, который позволяет работать с отдельными точками, изображенными на конкретном графике, не затрагивая всю таблицу исходных данных. Мы можем, например, интерактивно исключать некоторые «подозрительные» точки из процедуры подгонки и наблюдать за изменением аппроксимирующей функции.

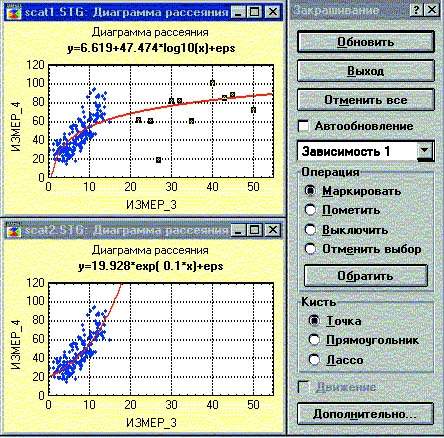Рис. 3. Интерактивное закрашивание (до и после удаления группы точек)

На левом фрагменте из рис. 3 более темным цветом выделены те точки, которые очевидно искажают характер аппроксимирующей кривой. Если с помощью процедуры закрашивания мы удалим эти «неудачные» точки из данного графика, то вид зависимости заметно изменится, фактически она превратится из логарифмической в экспоненциальную.

Режим закрашивания позволяет экспериментировать с конкретным графиком, не изменяя данные в исходной таблице, при этом выбранные точки можно маркировать, обозначать метками или исключать из процедуры подгонки. Таким образом, функция закрашивания представляет собой еще один важный и очень удобный метод графического разведочного анализа, который позволяет исследовать данные в интерактивном режиме.

Вращение трехмерных изображений

Для представления сложных зависимостей во многих случаях целесообразно использовать трехмерные или четырехмерные (тернарные) изображения. Поскольку отображение трехмерного графика на плоскости задается указанием угла зрения и перспективой, очень важной функцией является возможность интерактивного вращения трехмерной картинки (рис. 4).

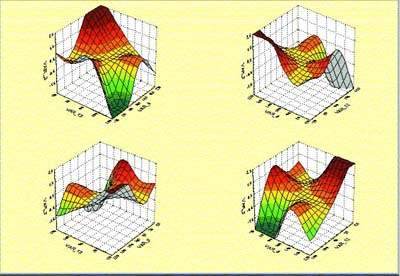Рис. 4. Интерактивное вращение трехмерного графика

С помощью такого инструмента можно взглянуть на график с разных сторон и выбрать именно тот вариант, который наилучшим образом отображает исследуемую структуру зависимостей.

Более того, часто именно вращение изображения помогает выявить скрытую форму кривой или поверхности, особенно если оно сочетается с возможностью изменения перспективы.

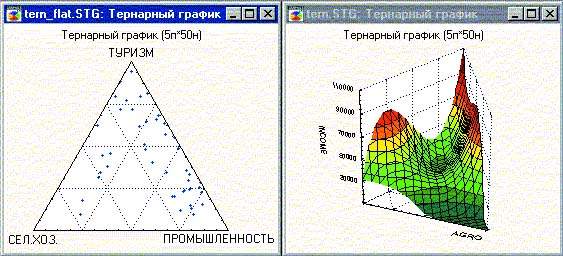
Рассмотрим теперь четырехмерные графики с четырьмя осями для четырех различных переменных, которые первоначально были придуманы для химических исследований по составлению смесей. Речь идет о так называемых тернарных графиках или графиках в треугольных координатах, когда на значения переменных накладываются определенные ограничения. Представим себе, что у нас имеются некоторые статистические данные о средних доходах населения в разных регионах, а также данные о том, какую долю в общем валовом продукте каждого региона составляют промышленность, сельское хозяйство и туризм. При этом мы условно считаем, что эти три группы включают в себя все сферы деятельности и в совокупности дают 100% валового продукта. Таким образом, значения трех переменных: доля промышленности, доля сельского хозяйства и доля туризма для каждого наблюдения (в данном случае региона) в сумме составляют постоянную величину, а именно 100%. Это и есть необходимое условие для построения тернарного графика (рис. 5).

Рис. 5. График на плоскости в треугольных координатах (слева) и тернарная поверхность

Все точки располагаются внутри равностороннего треугольника, в вершинах которого одна из переменных принимает максимальное значение (100%), а остальные равны нулю. На тернарной поверхности значения четвертой переменной изображены в зависимости от соотношения трех других. На графике (рис. 5) видно, что наименьшие значения среднего дохода наблюдаются в регионах, где в структуре отраслей преобладает сельское хозяйство.

Итак, тернарные графики представляют собой специфический, но весьма эффективный способ четырехмерного представления зависимостей, а их применение вовсе не ограничивается сугубо техническими приложениями.

Пиктографики

Можно ли теперь графически представить зависимость между большим числом переменных? Именно для этих целей и был разработан весьма непростой, но интересный метод - построение графиков из пиктограмм (пиктографиков).

Рис. 6. Пиктографики

На таких графиках (рис. 7) каждое наблюдение представлено в виде многомерного символа, элементы которого соответствуют значениям определенных переменных. Главная идея такого метода анализа основана на способности человеческого мозга «автоматически» выделять характерную структуру связей между многими элементами, если они представлены в определенной последовательности. Иногда понимание (или даже «ощущение») того, что некоторые элементы «чем-то похожи» друг на друга, приходит раньше, чем наблюдатель может объяснить, какие именно переменные определяют это сходство. На рис. 6 приведено несколько пиктографиков различных типов, построенных для одного и того же набора данных, при этом имеется возможность выбрать тип пиктограмм, наиболее выразительно отображающих структуру исследуемых взаимосвязей

Один из видов пиктографиков - это диаграмма «Лица Чернова». На такой диаграмме значения переменных поставлены в соответствие определенным чертам человеческого лица: размеру глаз, форме рта, длине носа и так далее. На графике (рис. 7) отображены результаты опроса людей различного возраста и образования по поводу их удовлетворенности собственной работой и семейным положением. При этом размеру лица соответствует годовой доход, размеру носа - уровень образования, а форме рта - оценка удовлетворенности работой. Обратите внимание, что на этой картинке лица большего размера имеют, как правило, и более длинный нос. Это означает, что уровень образования прямо влияет на доходы.

Рис. 7. Категоризованные тернарные графики и графики поверхности

Заметим еще, что большие лица чаще «улыбаются», а маленькие - «грустят». Это подтверждает тот очевидный факт, что те, кто имеет большие доходы, в большей степени удовлетворены своей работой. Рядом представлен тот же график, только с пиктограммами в виде звезд. Здесь мы можем увидеть и выделить группы наблюдений, имеющих похожие соотношения между переменными. Подобный метод можно рассматривать как графический аналог кластерного анализа, и он часто оказывается весьма эффективным на начальной стадии исследования. Дальнейший анализ данных, основанный на изучении интуитивно обнаруженного сходства, позволяет выявить конкретную природу проявившихся взаимосвязей между переменными.

Несмотря на то, что идея метода вполне понятна и прозрачна, ее практическое использование требует от исследователя определенного опыта и даже фантазии.

Но те, кто в полной мере овладел всеми тонкостями процедуры графического анализа, получают в свое распоряжение интересный и эффективный метод исследования.

Категоризованные графики

Работая в системе STATISTICA, пользователь имеет в своем распоряжении еще одну группу графических методов, играющих важную роль как в статистическом анализе данных, так и во многих других приложениях. Речь идет о возможности разбиения данных на группы и построении так называемых категоризованных графиков. Имеем ли мы результаты опросов, данные эксперимента, временные зависимости или таблицу показателей, в большинстве случаев значения переменных можно разбить на отдельные категории. Кроме того, в данных часто присутствует специальная переменная, содержащая небольшое число различных целых значений, которая называется категориальной и специально предназначена для распределения переменных по группам. Возможность быстрого построения графиков, которые можно было бы одновременно сравнивать и анализировать сразу для нескольких групп переменных, чрезвычайно удобна для исследователя. Даже если в данных нет явно выделенной категориальной переменной, можно задать специальные условия выделения подгрупп, используя для этого любые диапазоны значений. На таких графиках можно проследить характерные особенности отдельных групп наблюдений, объединенных в одном наборе данных.

Фактически с помощью разделения на группы мы можем графически изобразить связь между большим числом переменных, чем на некатегоризованном графике аналогичного типа. При этом для построения категоризованной гистограммы можно использовать три, а для категоризованной диаграммы рассеяния четыре переменные. Если построить категоризованный тернарный график, то можно представить связь между пятью переменными одновременно.

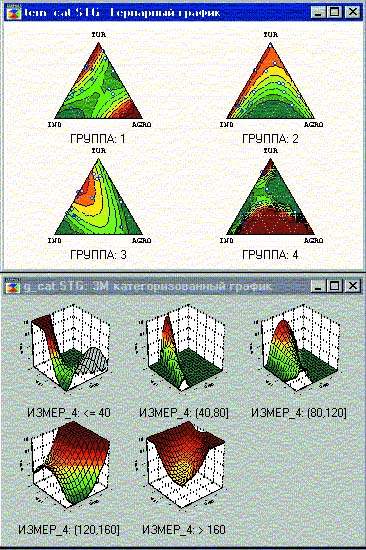
Вернемся теперь к данным, по которым был построен простой тернарный график. Тогда данные на группы не разделялись, а строилась одна зависимость для всех наблюдений. Теперь будем учитывать тот факт, что в файле объединены данные, полученные четырьмя разными способами. С помощью одной из переменных, в которой записана принадлежность наблюдений той или иной категории, построим категоризованный тернарный график для четырех групп.

Взглянув на полученный график (рис. 7), мы увидим, что структура данных в разных подгруппах различна. Это означает, что в данном случае способ расчета влияет на результат.

Категоризованные графики можно строить для гистограмм, диаграмм рассеяния карт линий уровня, вероятностных и других графиков, указав в соответствующем диалоговом окне необходимый набор параметров. Построив одновременно целый набор поверхностей (рис. 7), мы снова можем убедиться, насколько удобно иметь в программе возможность автоматического создания категоризованных графиков, где пользователь должен только перечислить интересующие его переменные и при необходимости задать метод категоризации, если его не устаивает тот, который программа использует по умолчанию.

Интересные варианты предлагаются пользователю и при построении категоризованных круговых диаграмм. Сама по себе круговая диаграмма это очень распространенный тип графического представления. Построим круговую диаграмму первой переменной для нескольких категорий значений третьей переменной нашего файла. Здесь, как и на любом категоризованном графике, мы получим просто набор диаграмм по числу заданных групп (левый график).

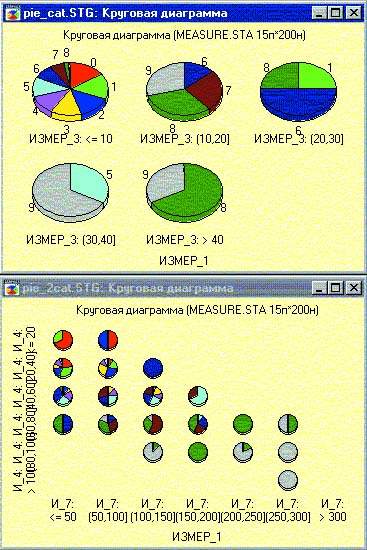Рис. 8. Круговые диаграммы

Если же задать не одну, а две группирующие переменные, то на экране появится очень интересная картинка, подобная той, что показана справа на рис. 8. Такой график фактически представляет собой диаграмму рассеяния для двух переменных, на которой каждая точка еще является круговой диаграммой значений третьей переменной.

Подобный способ представления данных может в некоторых случаях оказаться гораздо эффективнее, чем обычный трехмерный график, особенно если переменные содержат ограниченный набор целочисленных значений.

В статье были рассмотрены только несколько наиболее интересных и нетрадиционных вариантов графического анализа. Пользователь, занимающийся статистической обработкой данных в системе STATISTICA, имеет в своем распоряжении более сотни различных типов графического представления данных. Доступны практически все возможные типы графиков. В первую очередь это, конечно, полный набор традиционных гистограмм и диаграмм рассеяния, как двумерных, так и трехмерных, графики поверхностей и карт линий уровня, спектральные и трассировочные диаграммы.

Пользователю здесь предоставлен и максимальный доступ к настройке параметров графического изображения. Можно полностью регулировать отображение линий сетки, контурных линий и сечений поверхности, задавать расположение графика в окне, редактировать заголовки и подписи на осях. В графическое окно можно поместить любой текст, фигуры, произвольные рисунки и графические объекты в любом формате, доступном в системе Windows. В системе реализованы и другие важные для пользователя функции, например, автоматическое создание отчета о результатах анализа данных со всеми построенными в процессе работы графиками.

Об авторe