Художественное моделирование сложных трехмерных форм — это одна из наиболее сложных задач в компьютерном искусстве (computer art), а методы скульптурного моделирования заняли сегодня центральное место в машинной графике [1,2]. Так Д.Кескис (D.Keskeys) [1], например, утверждает, что "система, которая позволяет изменять форму воображаемого компьютерного материала путем резьбы по его поверхности, лепки и моделирования, открыла бы новые и волнующие перспективы для творчества". В данной статье мы рассмотрим два аспекта художественного моделирования геометрических форм.
1) Задание формы с помощью данных по глубине с последующей проекцией на базисную модель, на поверхности которой должна производиться резьба. Существующие системы рисования в трехмерном пространстве позволяют подготовить такие даные [3, 4], которые могут быть использованы для изменения положения соответствующих вершин полигонального представления, моделирующего резную поверхность [5].
2) Локальные изменения основной модели с использованием теоретико-множественных операций над ней и моделью резца. Этот метод был, например, реализован в интерактивном воксельном моделировании [6].
Здесь мы предлагаем средства художественного компьютерного моделирования, основанные на использовании функционального представления (F-rep), объединяющего такие разные по природе геометрические модели как теоретико-множественные твердые тела, воксельные объекты, заметания, неявно заданные поверхности на базе скелетонов и осевые объекты (medial axis) [7,8]. В принципе, любой объект, задаваемый с помощью неравенства вида f(x,y,z) > 0, может быть включен в эту модель.
Моделирование резьбы
Под резьбой мы понимаем создание новой трехмерной геометрической формы путем вырезания или гравировки по поверхности существующего объекта. Различаются следующие типы резных объектов: узорчатые решетки или розетки, рельефная резьба, а также скульптуры и гравировки, сделанные с помощью резцов, чеканов и прочих режущих, рубящих и колющих инструментов. Для каждого такого типа имеются свои процедурные модели и интерактивные средства.
Процедурные модели резьбы
Процедурное задание резного объекта начинается с графического изображения узора резьбы с целью сформировать вещественную функцию, задающую трехмерный объект. Моделирование узорчатых решеток выполняется в следующем порядке (рис. 1).
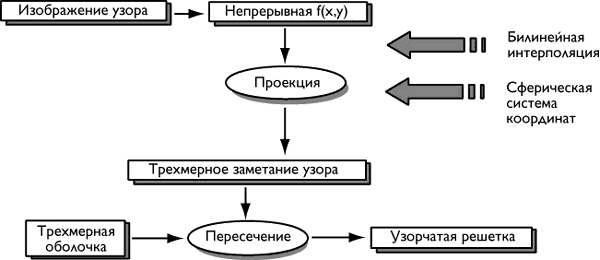
Рис. 1. Схема моделирования узорчатых решеток
- С помощью билинейной интерполяции (или интерполяции высшего порядка) создается непрерывная функция двух переменных, описывающая двумерную модель планируемого узора.
- Определяется трехмерный объект — основа будущей решетки ( например, тонкая оболочка).
- Задается операция проецирования с использованием цилиндрической, сферической или иной координатной систем.
- С помощью операции проецирования создается трехмерное заметание узора.
- Объект-основа пересекается с трехмерным заметанием узора, что приводит к созданию результирующего трехмерного объекта — узорчатой решетки.
Эти шаги описаны в виде операций над вещественными функциями, что собственно и задает процедурную F-rep модель резного объекта. На рис. 2 изображена смоделированная таким образом розетка.

Рис. 2. Трехмерная розетка
В случае моделирования рельефной резьбы мы также начинаем с двумерного изображения (штриховой рисунок либо полутоновое изображение) и создаем данные по глубине резьбы (рис. 3). Собственно резьба моделируется с помощью офсеттинга вдоль нормали, в котором величина офсеттинга определяется данными о глубине. Офсеттинг может быть применен к произвольному трехмерному объекту при условии, что у него можно вычислить нормаль в любой точке, заданной на его поверхности. Для функционально заданных объектов офсеттинг вдоль нормали переформулирован с использованием градиента описывающей функции.
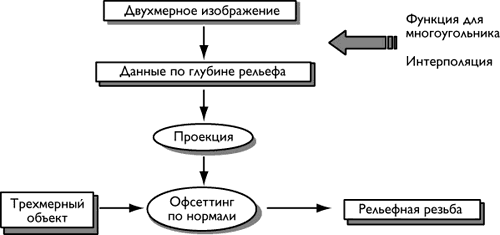
Рис. 3. Схема моделирования рельефной резьбы
Здесь используется две процедуры для создания данных по глубине: получение функции для многоугольника и зависящую от растрового шаблона интерполяцию.
Произвольный двумерный многоугольник (выпуклый или невыпуклый) может быть описан с помощью вещественной функции f(x,y), которая равна нулю на сторонах многоугольника. В этом случае проблема получения функции для многоугольника сводится к следующему. Простой двумерный многоугольник определяется как конечный набор отрезков. Эти отрезки задают стороны, а их концевые точки - вершины многоугольника. Многоугольник называется простым в том случае, если только соседние стороны имеют общую точку. Алгоритм получения вещественной функции для многоугольника должен удовлетворять следующим требованиям:
- он должен обеспечивать точное описание многоугольника в точках, где вещественная функция равна нулю;
- внутри и снаружи многоугольника не должно быть точек, в которых функция f(x,y) равна нулю;
- обработка каждого отдельно взятого многоугольника не должна требовать дополнительной информации.
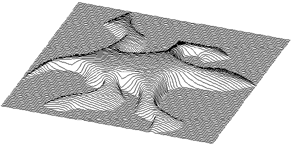
Для получения такого функционального описания мы используем монотонные теоретико-множественные выражения с R-функциями [9]. Затем положительные значения функции внутри многоугольника используются как данные по глубине. (рис. 4а). Офсеттинг вдоль нормали модулируется этими данными и применяется к произвольному твердому телу. Тем самым выполняется рельефная резьба (рис. 4б).
 |
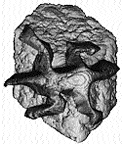 |
| Рис. 4. Рельефная резьба: а) моделирование данных по глубине с помощью процедуры, генерирующей функцию для многоугольника, б) резная ящерица на камне, выполненная с помощью офсеттинга вдоль нормали в соответствии с данными по глубине. | |
Другой способ получения данных по глубине использует зависящую от растрового шаблона интерполяцию нерегулярных данных с помощью метода конечных элементов, что позволяет совершить гладкую аппроксимацию для исходного изображения. Входными двумерными данными являются точки графического изображения резьбы. Каждая такая точка характеризуется координатами (x,y) и некой скалярной величиной. Например, это может быть 0 для черного и 255 для белого цветов. Простые интуитивные методы, такие как размывание границ (blurring), не могут обеспечить гладкой рельефной резьбы. Применение же метода конечных элементов для аппроксимации нерегулярных точек исходного изображения дает некоторые дополнительные преимущества по контролю формы резного объекта с помощью параметра гладкости. Алгоритм предполагает следующие шаги:
- задание исходных данных в случайном наборе точек плоскости;
- сортировка данных. На этом этапе исходные данные сносятся в узлы заданного растрового шаблона;
- решение задачи конечно-элементной аппроксимации.
- билинейная интерполяция данных для вычисления значений в заданных точках, например, в узлах густой прямоугольной сетки.
Описанный метод предполагал, что размерность исходного изображения меньше, чем размерность конечного изображения. В этом случае проблема сводится к вычислению величин цвета и интенсивности для каждого отдельного пиксела конечного изображения. Время выполнения указанных шагов на обычной графической рабочей станции равно примерно 1 сек. Величины, полученные на конечной регулярной сетке, используются в качестве данных по глубине для вырезания изображения на поверхности заготовки. На рис. 5 приведено изображение рельефной резьбы, полученной с помощью данных по глубине, взятых из штрихового рисунка с использованием описанной интерполяционной схемы.
 |
 |
| Рис. 5. Рельефная резьба: а) резьба с помощью данных по глубине с использованием интерполяции, зависящей от растрового шаблона, б) увеличенный фрагмент резьбы | |
Интерактивная резьба и чеканка
Опишем теперь еще одно применение вещественных функций для художественного моделирования. Художник работает виртуальными резцами и чеканами разных форм и размеров, выбирая их из имеющегося стандартного набора. При необходимости можно смоделировать нестандартный инструмент, меняя параметры его функциональных моделей. Выполняя резьбу или чеканку, художник работает так же, как он привык это делать, работая с настоящими инструментами. Виртуальная заготовка располагается под удобным углом наблюдения, выбирается и применяется нужный инструмент, а результат сразу виден на экране.
Если результат не нравится, то можно вернуться на шаг назад без всякого необратимого ущерба. Программа представляет собой систему интерактивного моделирования твердых тел, в которой заметания резцов последовательно вычитаются из заготовки или добавляются к ней. Все инструменты и сама заготовка смоделированы функционально с помощью вещественных функций. Операции реализованы путем вычитания, объединения и гладкого сопряжения (blending) твердых тел. Результирующий объект может быть представлен в качестве двоичного дерева, где каждый узел определяет теоретико-множественную операцию, а в конечных узлах заданы заметания инструментов. На рис. 6 изображены результаты интерактивной резьбы и чеканки: рис. 6а — результат резьбы полукруглыми резцами по поверхности воксельной модели человеческой головы, функциональная модель которой задана с помощью трилинейной интерполяции на значениях, определенных для вокселов; рис. 6б — чеканка по металлу, использованы операции вычитания и объединения с круглыми чеканами. Центральный объект сделан с помощью операции гладкого сопряжения нескольких полусфер, что моделирует используемый в чеканке метод поднятия рельефа с оборотной стороны листа металла. Узор фона сформирован ударами виртуального чекана с полусферической головкой. На рис. 6в приведен простой пример лепки, где сферическая заготовка сначала режется с применением операции сопряжения, что позволяет избавиться от острых краев, а затем производится дополнительное поднятие рельефа путем обычного объединения.
 |
 |
 |
| Рис. 6. Результаты интерактивной резьбы и чеканки: a) резьба полукруглыми резцами по поверхности воксельной модели человеческой головы, б) чеканка, в) лепка | ||
Для визуализации результата используется интерактивная трассировка лучей. Учитывая, что типовая модель может содержать несколько тысяч отдельных твердых тел, вычтенных или объединенных с заготовкой, легко предвидеть, что обычная трассировка лучей может потребовать значительных временных затрат - при трассировке каждого отдельного луча необходимо вычислять значение очень сложной функции, являющейся суперпозицией функций инструментов, операций и функции заготовки. Для ускорения этого процесса можно перерисовывать лишь те части изображения, которые были подвержены результатам воздействия инструментов. Для определения зоны возможных изменений для каждого отдельного заметания резца определяется его габаритный объем, который должен быть больше заметаемого объема — если одновременно с теоретико-множественными операциями используется операция сопряжения то ее результат распространяется также на соседние области. Такой подход позволяет обеспечить требуемое время перерисовки изображения изменяемых областей (не более 0.5 сек для сложных моделей), тем самым гарантируя как интерактивность, так и требуемое высокое качество изображения без искажений формы, свойственных полигональным моделям. Конечная и промежуточные модели могут быть сохранены в формат системы POV-Ray [10,11]. Это позволяет использовать POV-Ray для последующей отрисовки смоделированной формы с максимально высоким качеством или для использования ее в других трехмерных сценах. В этой работе мы использовали расширение системы POV-Ray, которое позволяет изображать объекты описанные с помощью вещественных функций [12]. На рис. 7 приведены результаты трассировки смоделированных изображений чеканки и резьбы по крашеной деревянной доске.
 |
 |
| Рис. 7. Трассировка смоделированных форм с помощью POV-Ray: а) фото-реалистичная трассировка лучей результата интерактивной чеканки, б) резьба по крашеной деревянной доске. | |
Комплексный пример художественного моделирования
Описанные методы художественного моделирования могут применяться для моделирования сложных трехмерных геометрических форм и сцен в компьютерном искусстве. На рис. 8 изображена сцена, полностью смоделированная с использованием вещественных функций, включая модели резьбы.
 |
 |
| Рис. 8. Сцена "Геометрическое мышление", полностью смоделированная с помощью F-rep. | |
Перечислим теперь модели, которые использованы в этой сцене. Центральный объект сцены — голова с выдвижным ящиком в стиле С.Дали — смоделирована с помощью трилинейной интерполяции воксельных данных и теоретико-множественных операций над головой и функционально заданными геометрическими примитивами. Волосы смоделированы с помощью функционально опеределенных обобщенных цилиндров. Для моделирования прически применялись теоретико-множественные операции и нелинейные преобразования цилиндров. Подсвечник смоделирован уже описанным методом резьбы узорчатых решеток. Свеча смоделирована как цилиндр с отсеченной верхней частью, после чего к нему добавлены подтеки воска, определенные как осевые объекты. Стол и блюдо — тоже функционально определенные твердые тела. Объемные ящерицы, ползущие по ножке стола, выполнены с помощью рельефной резьбы. Фон с облаками сделан с помощью интерполяции разреженных данных, стилизованная комета — осевой объект. Трассировка сцены с помощью POV-Ray заняла несколько часов работы на станции SGI Indigo2.
***
В статье представлены новые методы моделирования узорчатых решеток, рельефной резьбы, чеканки и лепки, а также дано представление о системе интерактивного художественного моделирования. Все описанные методы объединены единой математической моделью функционального представления. Авторы полагают, что эти методы моделирования позволят художникам, работающим в области компьютерного искусства, открыть для себя новые источники трехмерных форм и операций.
На данный момент результатами работы наших программ является графическое изображение и описание трехмерной сцены с помощью F-rep и языка POV-Ray. В ближайшей перспективе будут получены трехмерные физические модели с помощью оборудования для быстрого изготовления прототипов (rapid prototyping).
Литература
- D.J. Keskeys "Computer sculpture - new horizons", Computer Graphics, vol. 28, 4:255-257, 1994.
- Special issue on interactive sculpting, J. Rossignac (Ed.), ACM Transactions on Graphics, vol. 13, 2, 1994.
- L. Williams "3D paint", Computer Graphics, vol.24, 2: 225-233, 1990..
- C.W.A.M. van Overveld "Painting gradients: free-form surface design using shading patterns", Graphics Interface '96, Canadian Human-Computer Communication Society, 1996: 151-158.
- C.K. Chua, R. Gay, W. Hoheisel "Computer aided decoration of ceramic tableware. Part I: 3-D decoration", Computers and Graphics, vol. 21, 5: 641-653, 1997.
- T. Galyean, J. Hughes "Sculpting: an interactive volumetric modeling technique", SIGGRAPH '91 proceedings: 138-148.
- A. Pasko, V. Adzhiev, A. Sourin, V. Savchenko "Function representation in geometric modeling: concepts, implementation and applications", The Visual Computer, vol.11,8:429-446, 1995.
- В.Аджиев, А.Пасько, В.Савченко, А.Сурин, "Моделирование форм с использованием вещественных функций", Открытые Системы, 5, 1996, с.14-18.
- A.A. Pasko, A.V. Savchenko, V.V. Savchenko. "Polygon-to-function conversion for sweeping", Eurographics/SIGGRAPH Workshop on Implicit Surfaces, Eindhoven, The Netherlands, 1996: 163-171.
- А. Сурин, "Трассировка лучей с помощью POV-Ray", //Открытые Системы, 6, 1997, с.38-42.
- POV-Ray homepage.
- R. Suzuki "POV-Ray 3 isosurface patch".
Александр Пасько(pasko@mail.com), Алексей Сурин, Владимир Савченко
