ДНК-компьютеры можно назвать утконосами компьютерного мира — столь необычен их вид, столь странны их компоненты. В числе прочих «деталей» ДНК-компьютеры включают в себя такие неэлектронные узлы, как пробирки, ферменты, пена и гели для электрофореза, бактерии E. Coli и, конечно, дезоксирибонуклеиновая кислота (ДНК).
ДНК-вычисления впервые были с успехом применены в 1994 году Леонардом Эдлеманом, профессором Университета Южной Калифорнии, для решения так называемой задачи коммивояжера. С того времени было создано несколько других прототипов. Все они использовались для проверки концепции путем решения упрощенных вариантов более крупных, более сложных задач.
 |
Маловероятно, что ДНК-компьютеры станут самостоятельными конкурентами своим электронным собратьям. Леонард Эдлеман, профессор Университета Южной Калифорнии |
Помимо своей оригинальности ДНК-вычисления привлекают к себе внимание еще и потому, что они используют вид массового параллелизма, который невозможно реализовать средствами электроники или даже оптики. «В пробирке» в параллель могут быть сгенерированы триллионы возможных вариантов.
Однако задачи, которые могут быть решены с помощью такого подхода, должны быть строго специфицированы. Ни один из существующих прототипов еще не позволяет утверждать, что подобная технология получит массовое применение.
Открытие
Эдлеман использовал ДНК при решении задачи коммивояжера для семи узлов. Эта задача состоит в следующем. Дан граф из семи узлов и соединяющих их направленных ребер. Можно ли определить путь, начинающийся в узле 0 и заканчивающийся в узле 6, так, чтобы он проходил через все остальные узлы только один раз?
Эта задача относится к проблемам резервирования ресурсов, и ее решение может оказаться полезным, к примеру, при планировании авиаперелетов.
Сообразительный старшеклассник с помощью ручки и листа бумаги может решить задачу для семи узлов намного быстрее, чем предложенный Эдлеманом ДНК-компьютер, который потратил на это около недели. Но представьте себе задачу коммивояжера для 200 узлов. Сложность подобных задач (математики называют их «NP-полными») растет экспоненциально.
Когда число узлов становится достаточно большим, обычные электронные компьютеры решить ее уже не в состоянии. С другой стороны, по некоторым оценкам, при использовании массового параллелизма в варианте ДНК-вычислений Эдлемана для решения задачи с 200 узлами может потребоваться ДНК-цепочка, вес которой превышает вес Земли.
При решении задачи для семи узлов Эдлеман присвоил ДНК-коды всем элементам графа, сопоставив один код каждому узлу и один код каждому направленному ребру. В пробирке он смешал комбинации этих кодов в ДНК-цепочки, каждая из которых представляла одного из претендентов на роль решения задачи. Затем Эдлеман отфильтровал неверные решения с помощью набора логических критериев, которые можно «применить» в пробирке.
Угроза безопасности
Такая методика в принципе позволяет решить любую задачу, постановка которой аналогична задаче, увлекшей Эдлемана.
Эдлеман и другие исследователи полагают, что этот метод может применяться для взлома «официального» американского стандарта на шифрование Data Encryption Standard, который используется для кодирования критически важных данных при их передаче. 56-разрядный ключ DES представляет для многих современных компьютеров очень непростую задачу.
Но метод на базе ДНК-вычислений, дающий возможность протестировать все 72 квадриллиона ключей одновременно, теоретически позволяет это сделать. Правда, специалисты по ДНК-вычислениям из компании RSA Data Security утверждают, что «достаточно большой ключ способен ?заблокировать? любой ДНК-компьютер, который только может быть создан».
Группа исследователей из NEC Research Institute в 1997 году сообщила о создании ДНК-компьютера для решения «задачи максимальной связности» для 6 узлов и 11 соединений. Задача звучит следующим образом. Дан набор узлов и набор соединений. Каково максимальное число узлов, которые можно связать напрямую?
Изучение позолоченных пластин
Ученые Университета штата Висконсин использовали другой тип ДНК-компьютера для решения «задачи выполнимости», при которой проверяется, удовлетворяют ли наборы двоичных значений формуле, и в результате порождается двоичное значение «истины».
В этом случае нити ДНК размещались на стекле с золотым покрытием так, чтобы ДНК-решение не было случайно смыто. Неверные решения отбраковывались и смывались.
Большинство этих схем ДНК-вычислений предполагают разрушение ДНК-компьютера после решения задачи. В отличие от электронных команд, выполнение которых, нажав кнопку, можно начать сначала, ДНК-компьютер требует несопоставимо более сложной «инициализации».
Программист, который привык для отладки кода снова и снова запускать разные варианты программы, должен принять новую парадигму. Если в электронной среде появление дополнительного условия о том, чтобы коммивояжер Эдлемана посетил один из узлов дважды, причем не указывая, какой именно из узлов, требует простых изменений в алгоритме, то в ДНК-среде это может потребовать создания полностью новой системы фильтрации и сортировки и, возможно, иного подхода к постановке задачи.
«Маловероятно, что ДНК-компьютеры станут самостоятельными конкурентами своим электронным собратьям», — считает Эдлеман.
По мнению Джона Рейфа, профессора факультета информатики Университета Дюка, самой перспективной областью применения таких компьютеров может стать упрощение декодирования и обработки естественных ДНК, которые ведутся в рамках проекта изучения генома человека Human Genome Project и в лабораториях экспертов-криминалистов.
ДНК-вычисления: шаг за шагом
На этом рисунке представлен алгоритм, который Эдлеман использовал для решения задачи коммивояжера для семи узлов. Весь процесс решения занял около семи дней
Задача
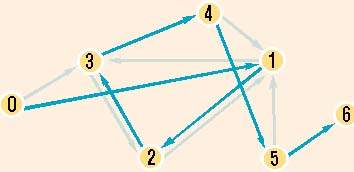
Задача коммивояжера для семи узлов, решенная на ДНК-компьютере, созданном Леонардом Эдлеманом. Решение показано зеленым цветом, а узлы помечены в порядке их посещения: 0?1?2?3?4?5?6
«Вычислительная» установка
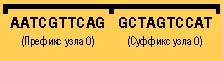
I Каждому узлу присваивается код из 20 оснований. Основания состоят из четырех нуклеотидов ДНК (обозначенных как A, T, C и G); префикс и суффикс каждого узла должны быть уникальны.
Например, код узла 0 может выглядеть следующим образом:
II ДНК, представляющие каждое из направленных ребер, генерируются из кодов узлов. Суффикс узла, из которого выходит ребро, присоединяется к префиксу узла, в которое это ребро входит.
Например, ребро, выходящее из узла 0 и входящее в узел 1, будет иметь вид:
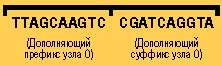
III Для ДНК-кода каждого узла, присвоенного на шаге 1, генерируются дополняющие коды. Дополняющая ДНК — это ДНК, которая связана с другой нитью ДНК, то есть образует двойную цепочку. Нуклеотиды A связаны с нуклеотидами T, а нуклеотиды C — с нуклеотидами G.
Дополняющая ДНК для этого примера будет иметь вид:
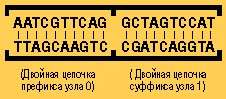
Если две нити ДНК смешаны вместе, то они могут связаться следующим образом:
IV В пробирке смешиваются ДНК ребра и дополняющая ее ДНК. Если эти нити могут образовать двойную цепочку, то она будет образована.
Например, дополняющая ДНК для узла 0 может образовать двойную цепочку с частью ДНК для ребра, соединяющего узел 0 с узлом 1:
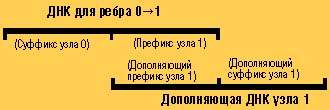
Вычисления
Эта нить может затем образовывать двойную цепочку с любой нитью для ребра, начинающейся с суффикса узла 1. Как показано в данном примере, она образует двойную цепочку с ДНК для ребра, выходящего из узла 1 в узел 3*.
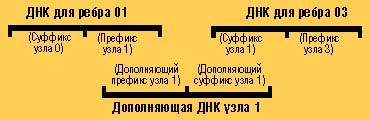
Отметим, что для поставленной в данном примере задачи не существует ребер, входящих в узел 0, и ребер, выходящих из узла 6. Опираясь на этот факт, Эдлеман использовал разряды ДНК, содержащие либо суффикс узла 0, либо префикс узла 6, и ферменты для того, чтобы размножить все цепочки ДНК, начинающиеся с узла 0 или заканчивающиеся узлом 6. Таким образом, на последующих шагах было проще манипулировать «правильными» ДНК: образец оказался бы достаточно большим и вряд ли был бы утрачен в результате случайной утечки.
* В данном примере для организации цепочки была использована «ошибочная» ДНК ребра, поэтому данная цепочка в результате будет отвергнута.
ОТВЕТ
После того как ДНК выращивались необходимое количество времени при нужной температуре, и набор ответов, в состав которого входил «верный», был размножен, «неверные последовательности» были отсеяны.
V ДНК-последовательности, которые начинаются не с узла 0, отфильтровываются. Также отфильтровываются ДНК-последовательности, которые не заканчиваются на узле 6.
VI ДНК-последовательности фильтруются по длине. Сохраняются только те последовательности, которые имеют семь узлов с 20 основаниями.
VII Все ДНК-последовательности, которые не содержат ДНК узла 2, отфильтровываются. Также отфильтровываются все ДНК-последовательности, которые не содержат ДНК узлов 3, 4 и 5.
VIII Если в результате осталась хотя бы одна ДНК, то она обладает всеми нужными свойствами. То есть она начинается в узле 0, заканчивается в узле 6, включает в себя все узлы и имеет длину, которая означает, что она содержит все шесть узлов, причем каждый из них только один раз. Разложение ДНК на цепочки позволяет определить порядок кодов и найти решение.